Приглашение в теорию чисел

F_n = 2^2ⁿ+1. (2.3.1)

Ферма был абсолютно уверен, что все числа этого вида являются простыми, хотя он не проводил вычислений других чисел, кроме указанных пяти. Однако это предположение было сдано в архив неоправдавшихся математических гипотез после того, как Леонард Эйлер сделал еще один шаг и показал, что следующее число Ферма

F₅ = 4 294 967 297 = 641 6 700 417

не является простым, что и показывает приведенная запись. Возможно, что этим история чисел Ферма была бы закончена, если бы числа Ферма не появились в совсем другой задаче, задаче построения правильных многоугольников при помощи циркуля и линейки.

Правильным многоугольником называется многоугольник, вершины которого лежат на некоторой окружности на одинаковых расстояниях друг от друга (рис. 13). Если у правильного многоугольника n вершин, то мы называем его правильным n- угольником.

Рис 13.

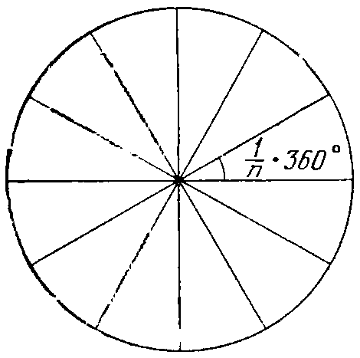
Если мы проведем n радиусов, соединяющих центр окружности с вершинами, то получим n центральных углов величиной 

1/n  360° 

каждый. Если можно построить угол, имеющий эту величину, то можно построить и этот n-угольник.

Древние греки очень хотели найти методы построения правильных многоугольников с помощью циркуля и линейки. Разумеется, они умели строить простейшие из них — равносторонний треугольник и квадрат. С помощью повторного деления пополам центрального угла они могли также построить правильные многоугольники с

4, 8, 16, 32…,

3, 6, 12, 24…

вершинами. Кроме того, они умели строить правильный пятиугольник, и следовательно, также правильные многоугольники с

5, 10, 20, 40…

вершинами. Был также получен еще один тип правильного многоугольника. Центральный угол в правильном 15-угольнике равен

1/15 360° = 24°,

и он может быть получен с помощью утла в 72°, соответствующего правильному пятиугольнику, и угла в 120°, соответствующего правильному треугольнику, если удвоить первый угол и вычесть из него второй. Следовательно, мы можем построить правильные многоугольники с 15, 30, 60, 120… сторонами.

В таком состоянии проблема оставалась до 1801 года, когда вышла работа по теории чисел молодого немецкого математика К. Ф. Гаусса (1777–1855) «Арифметические исследования». Она открыла новую эпоху в математике. Гаусс превзошел греческих геометров не только в том, что указал метод построения циркулем и линейкой правильного 17-угольника, но и пошел гораздо дальше. Для всех чисел n он определил, какие n-угольники могут быть построены таким образом, а какие нет. Сейчас мы опишем результаты, полученные Гауссом.

Выше мы отмечали, что из правильного n-угольника можно получить правильный 2n-угольник, деля каждый центральный угол пополам. С другой стороны, из 2n-угольника можно получить n-угольник, используя лишь каждую вторую вершину. Это показывает, что достаточно провести поиск правильных многоугольников, которые могут быть построены с помощью циркуля и линейки, только среди многоугольников с нечетным числом вершин. Гаусс доказал, что правильный n-угольник с нечетным числом вершин может быть построен с помощью циркуля и линейки тогда, и только тогда, если число n является простым числом Ферма или произведением нескольких различных простых чисел Ферма.

Что это нам дает для небольших значений n? Очевидно, что 3-угольник и 5- угольник могут быть построены, в то время как 7-угольник не может, так как 7 не является простым числом Ферма. Не может быть построен и 9-угольник, так как 9 = 3 • 3 является произведением двух равных простых чисел Ферма.

Открытие Гаусса, естественно, возродило интерес к числам Ферма (2.3.1). За последнее столетие были предприняты поистине героические поиски, вручную, без помощи машин, новых простых чисел Ферма. В настоящее время эти вычисления продолжаются со все возрастающей скоростью с помощью ЭВМ. Однако до сих пор результаты были отрицательными. Ни одного нового простого числа Ферма не было найдено и сейчас многие математики склонны считать, что их больше нет.

Система задач 2.3.

1. Найдите все нечетные числа n < 100, для которых можно построить правильный n-угольник.

2. Как построить правильный 51-угольник, имея правильный 17-угольник?

3. Если не существует простых чисел Ферма, кроме выше указанных пяти, то сколько существует правильных n-угольников (n нечетно), которые могут быть построены циркулем и линейкой? Каково то наибольшее нечетное n, для которого может быть построен правильный n- угольник?

§ 4. Решето Эратосфена

Как мы уже говорили, существуют таблицы простых чисел, простирающиеся до очень больших чисел. Как можно было бы подступиться к составлению такой таблицы? Эта задача была, в известном смысле, решена (около 200 г. до н. э.) Эратосфеном, математиком из Александрии. Его схема состоит в следующем: напишем последовательность всех целых чисел от 1 до числа, которым мы хотим закончить таблицу:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
       2   2   2  3  2     2      2  3

Начнем с простого числа 2. Будем выбрасывать каждое второе число, начиная с 2 (кроме самого числа 2), т. е. чётные числа 4, 6, 8, 10 и т. д., подчеркивая каждое из них. После этой операции первым неподчёркнутым числом будет число 3. Оно простое, так как не делится на 2. Оставив число 3 неподчёркнутым, будем подчеркивать каждое третье число после него, т. е. числа 6, 9, 12, 15…; некоторые из них уже были подчеркнуты, поскольку они являются чётными. На следующем шаге первым неподчёркнутым числом окажется число 5; оно простое, так как не делится ни на 2, ни на 3. Оставим число 5 неподчёркнутым, но подчеркнем каждое пятое число после него, т. е. числа 10, 15, 20, 25…; как и раньше, часть из них уже оказалась подчёркнутой. Теперь — наименьшим неподчёркнутым числом окажется число 7. Оно простое, так как не делится ни на одно из меньших его простых чисел 2, 3, 5. Повторяя этот процесс, мы в конце концов получим последовательность неподчёркнутых чисел; все они (кроме числа 1) являются простыми.

Этот метод отсеивания чисел известен как «решето Эратосфена». Любая таблица простых чисел создается по этому принципу решета. В действительности, можно продвинуться гораздо дальше по ряду простых чисел, если использовать для их хранения память ЭВМ. Подобным образом, в Научно- исследовательской лаборатории Лос-Аламоса были получены все простые числа до 100 000 000.