The Clockwork Rocket

APPENDIX 2

LIGHT AND COLORS

The names of colors are translated so that the progression from “red” to “violet” implies shorter wavelengths. In the Orthogonal universe this progression is accompanied by a decrease in the light’s frequency in time. In our own universe the opposite holds: shorter wavelengths correspond to higher frequencies.

The smallest possible wavelength of light, ?_min, is about 231 piccolo-scants; this is for light with an infinite velocity, at the “ultraviolet limit”. The highest possible time frequency of light, ?_max, is about 49 generoso-cycles per pause; this is for stationary light, at the “infrared limit”.

All the colors of light arise from the same pattern of wavefronts, rotated into different orientations in four- space.

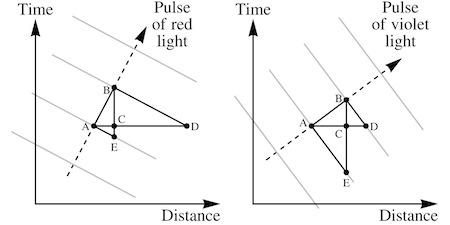
In the diagram above, AB is the separation between the wavefronts in four-space, which is fixed regardless of the light’s color. AD is the light’s wavelength (the distance between wavefronts at a given moment) and BE is the light’s period (the time between wavefronts at a fixed location).

The right triangles ACB and ABD are similar triangles, because the angles at A are the same. It follows that AC/AB = AB/AD, and:

AC = (AB)²/AD

Also, the right triangles ACB and EAB are similar, because the angles at B are the same. It follows that BC/AB = AB/BE, and:

BC = (AB)²/BE

Pythagoras’s Theorem, applied to the right triangle ACB, gives us:

(AC)² + (BC)² = (AB)²

Combining these three results yields:

(AB)⁴/(AD)² + (AB)⁴/(BE)² = (AB) ²

If we divide through by (AB)⁴ we have:

1/(AD)² + 1/(BE)² = 1/(AB)²

Since AD is the light’s wavelength, 1/AD is its spatial frequency, ?, the number of waves in a unit distance. Since BE is the light’s period, 1/BE is its time frequency, ?, the number of cycles in a unit time. And since AB is the fixed separation between wavefronts, 1/AB is the maximum frequency of light, ?_max, the frequency we get in the infrared limit when the period is AB.

So what we’ve established is that the sum of the squares of the light’s frequencies in space and in time is a constant:

?² + ?² = ?_max²

This result assumes that we’re measuring time and space in identical units. But in the table above we’re using traditional units that pre-date Yalda’s rotational physics. The data Yalda gathered on Mount Peerless showed that if we treat intervals of time as being equivalent to the distance blue light would travel in that time, the relationship between the spatial and time frequencies takes the simple form derived above. So the appropriate conversion factor from traditional units to “geometrical units” is the speed of blue light, v_blue, and we have:

(v_blue ? ?)² + ?² = ?_max²

The values in the table are expressed in a variety of units that have been chosen so that the figures all have just two or three digits. When we include a factor to harmonise the units, the relationship becomes:

(78/144 ? ?)² + ?² = ?_max²

Now, the velocity, v, of light of a particular color is simply the ratio between the distance the light travels and the time in which it does so. If we take the pulses of light in our first diagram, they travel a distance AC in a time BC, giving v = AC/BC. If we then use the relationships we’ve found between AC and AB and the spatial frequency ?, and between BC and BE and the time frequency ?, we have:

v = ?/?

Again, we can only use this formula with traditional units after applying the appropriate conversion factor:

v = (v_blue ? ?)/?

which, if we’re taking frequencies from the table above, becomes:

v = (78/144 ? ?)/?

The velocity we’ve been describing so far is a dimensionless quantity, related to the slope of a line tracing out the history of the light pulse on a space-time diagram. (The way we draw our diagrams, with the time axis vertical and the space axis horizontal, it’s actually the inverse of the slope.) Multiplying the dimensionless velocity by a further factor of 78, the speed of blue light in severances per pause, gives us the values in traditional units that