повторяются через 400 лет.
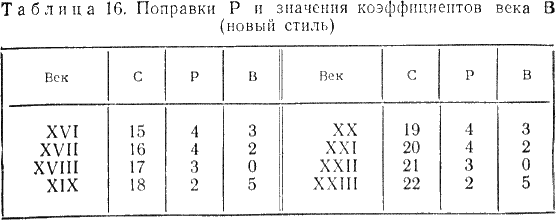
С введением григорианского календаря появились особые простые вековые годы 1700, 1800, 1900; для которых коэффициент года Г, определяемый по формуле (6), необходимо уменьшать на единицу, т. е. для этих лет
Г = |(100+ [100:4])/7 | = 5.
Что касается вековых лет, число сотен которых кратно четырем, например, 1600, 2000 и т. д., то для нового стиля они остаются високосными, и коэффициент года для них определяется по общему правилу:
Г = |(
Итак, порядковый номер d дня недели любой календарной даты задается формулой (1) (см. с. 102). Значение коэффициента месяца М берется из табл. 15, коэффициент года Г вычисляется по формуле (6) или (7), а значение коэффициента века В берется для старого стиля из табл. 14, а для нового из табл. 16. Напомним еще раз, что если сумма К + М + Г + В меньше семи, то остаток от деления на семь равен самой сумме. То же правило действует при делении на четыре.

§ 24. Исследование календарных формул
Начиная с 1873 года календарные формулы публиковались в разных странах. Входящие в них элементы имели различные обозначения и порядок расположения. Для возможности исследования формул мы свели их в таблицу (табл. 17) в хронологическом порядке с одинаковыми условными обозначениями (см. § 23) и расположением элементов К, М, Г и В.

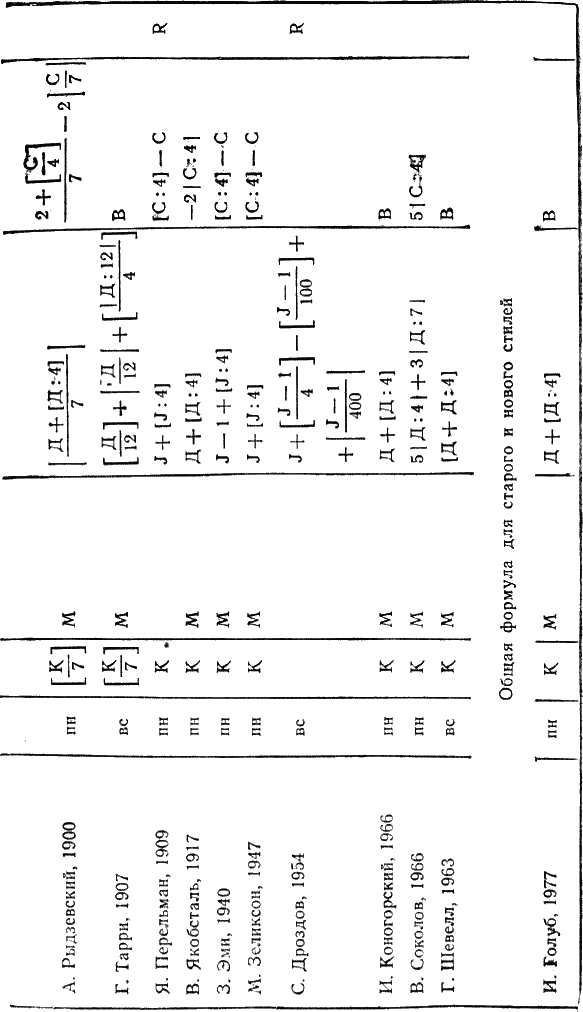
В большинстве формул коэффициент месяца М дается в виде таблицы с готовыми значениями — числами от 0 до 6. В некоторых формулах (Перевощиков, Дроздов и Перельман) вместо готовых значений коэффициента месяца М используется число дней от начала года R. Это усложняет вычисления. Также усложняет вычисления примененное Целлером и Каменьщиковым определение коэффициента месяца М в зависимости от порядкового номера месяца в году m (при этом январь и февраль високосного года считаются 13-м и 14-м месяцами предыдущего года). Формулы отличаются еще и тем, что при вычислении коэффициента года в одних вводится полный номер года J, а в других его порядковый номер в столетий Д, что упрощает вычисления.
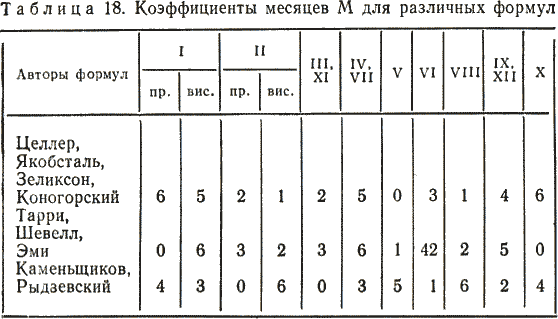
В табл. 18 приведены значения коэффициента месяца М для формул, представленных в табл. 17. Проверка показала, что все формулы дают правильные ответы для всех дат за исключением простых (невисокосных) вековых лет по новому стилю, — т. е. годов 1700, 1800, 1900, 2100, 2200, 2300 и т. д. Для этих годов необходимо уменьшать на единицу коэффициент года Г (см. формулу (7)).
§ 25. Постоянные табель-календари. Табель-календарь И. Я. Голуба
Определение дня недели значительно упрощается с помощью постоянных табель-календарей. Если подсчитать для каждого года и месяца заданного столетия величины Е, представляющие остатки от деления на 7 (т. е. числа от 0 до 6) суммы коэффициентов месяца М, года Г и века В,
Е = |(M + Г + B)/7 |,
и свести их в таблицу, то определение дня недели выразится формулой
d = |(К + Е)/7 |,
где К — календарное число месяца.
Каждый замечал, что распределение дней недели по числам года повторяется. Эта повторяемость имеет определенную закономерность. Так, если номер года в столетии при делении на 4 дает в остатке 1 (год, следующий за високосным), то следующий год с тем же распределением дней недели повторится через 6 лет, если же остаток 2 или 3, то следующий такой же год будет через 11 лет. Так, для 1985 г. (85 = 21 × 4 + 1) это будет год 1991, а для годов 1986 и 1987 (соответственно 21 × 4 + 2 и 21 × 4 + 3) — годы 1997 и 1998. Високосные годы с одинаковым распределением дней педели повторяются только через 28 лет. В юлианском календаре ровно через 100 лет даты отступают по дням недели на одну позицию назад, и полная повторяемость дней педели происходит через 700 лет. В григорианском календаре столетия начинаются только с воскресенья, субботы, четверга и вторника, и здесь полный цикл завершается по прошествии 400 лет.
В книге А. В. Буткевича и М. С. Зеликсона (см. список литературы) представлена обширная коллекция из 60 постоянных табель-календарей без их математического обоснования и подробного анализа. Рассмотрим их отличия. Часть из них рассчитана на старый стиль (юлианский календарь), а часть на новый стиль (григорианский календарь). Следует отметить, что табель-календарь на XX в. по новому стилю совпадает с календарем для XIX в. по старому стилю.
Другое отличие состоит в том, что в одних календарях для определения порядкового номера дня недели приходится находить остатки от деления на 7 суммы К + Е, а в других день недели определяется по таблице готовых значений этой суммы. Сумма К + Е имеет значения от 1 до 37, при этом значениям 1, 8, 15, 22, 29 и 36 соответствует один день недели, значениям 2, 9, 16, 23, 30, 37 — следующий и т. д. Такая таблица дается в ряде вечных календарей.
Еще одно отличие заключается в том, что в одних календарях приводятся 12 столбцов значений Е, а а других 7. Это следует из таблиц 11, 13, 15, в которых можно объединить также январь простого года и октябрь, январь високосного года и апрель, июль и т. д.
Остается определить, па какие сроки целесообразно издавать постоянные табель-календари. В книге А. В. Буткевича и М. С. Зеликсона такие календари подразделяются на краткосрочные со сроком действия от одного до 25 лет, среднесрочные (от 34 до 200 лет) и долгосрочные (200–3000 лет). По нашему мнению, наименьший срок, на который нужно рассчитывать постоянные табель-календари, — это столетие. Предлагаем постоянный табель-календарь на XX в. по новому стилю (табл. 19), состоящий из частей А и Б. Он пригоден также для XIX в. по старому стилю. Если к нему добавить таблицу поправок (табл. 20), то он будет пригоден для 1–2000 гг. по старому стилю и для 1501–2301 гг. по новому стилю. Для определения дня недели нужно взять значение Е на пересечении номера года в столетии с колонкой месяца для високосного или невисокосного года в части А и прибавить к нему число месяца К. По полученной сумме в части Б найдем день недели.


