Медицинская физика

В ряде медицинских измерений может быть недостаточной информация о связи между непосредственно измеряемой физической величиной и соответствующими медико-биологическими параметрами. Так, например, при клиническом (бескровном) методе измерения давления крови допускается, что давление воздуха внутри манжеты приблизительно равно давлению крови в плечевой артерии.

4. Случайная величина. Закон распределения

Определение случайной величины. Многие случайные события могут быть оценены количественно как случайные величины. Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретные и непрерывные случайные величины.

Распределение дискретной случайной величины. Дискретная величина считается заданной, если указаны возможные ее значения и соответствующие им вероятности. Обозначим дискретную случайную величину х, ее значения х₁, х₂…, в вероятности: Р (х₁) =р₂, Р (х2) = р₂ и т. д.

Совокупность х и Р называется распределением дискретной случайной величины.

Так как все возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна единице:

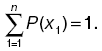
Здесь предполагается, что дискретная случайная величина имеет n значений. Выражение называется условием нормировки.

Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины. Наиболее употребительные из них: 1) математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений;

2) дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Для непрерывной случайной величины математическое ожидание и дисперсия записываются в виде:

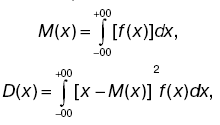
где f(x) – плотность вероятности или функция распределения вероятностей. Она показывает, как изменяется вероятность отнесения к интервалу dx случайной величины в зависимости от значения самой этой величины. Нормальный закон распределения. В теориях вероятностей и математической статистики, в различных приложениях важную роль играет нормальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность ее вероятности имеет вид:

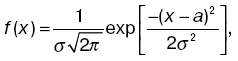
где а = М(х) – математическое ожидание случайной величины;

? – среднее квадратное отклонение; следовательно;

?²– дисперсия случайной величины. Кривая нормального закона распределения имеет колоколообразную форму, симметричную относительно прямой х = а (центр рассеивания).

5. Распределение Максвелла (распределение газовых молекул по скоростям) и Больцмана

Распределение Максвелла – в равновесном состоянии параметры газа (давление, объем и температура) остаются неизменными, однако микросостояния – взаимное расположение молекул, их скорости – непрерывно изменяются. Из-за огромного количества молекул практически нельзя определить значения их скоростей в какой-либо момент, но возможно, считая скорость молекул непрерывной случайной величиной, указать распределение молекул по скоростям. Распределение молекул по скоростям подтверждено различными опытами. Распределение Максвелла можно рассматривать как распределение молекул не только по скоростям, но и по кинетическим энергиям (так как эти понятия взаимосвязаны).

Выделим отдельную молекулу. Хаотичность движения позволяет например для проекции скорости Vx молекулы принять нормальный закон распределения. В этом случае, как показал Дж. К. Максвелл, плотность вероятности того, что молекула имеет компоненту скорости Ux, записывается следующим образом:

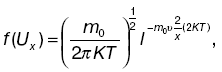
Можно получить максвелловскую функцию распределения вероятностей абсолютных значений скорости (распределение Максвелла по скоростям):

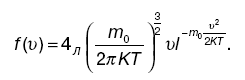
Распределение Больцмана. Если молекулы находятся в каком-либо внешнем силовом поле (например, в гравитационном поле Земли), то можно найти распределение по их потенциальным энергиям, т. е. установить концентрацию частиц, обладающих некоторым определенным значением потенциальной энергии. Распределение частиц по потенциальным энергиям в силовых полях – гравитационном, электрическом и др. – называют распределением Боль- цмана.

Применительно к гравитационному полю это распределение может быть записано в виде зависимости концентрации n молекул от высоты h над уровнем земли, или потенциальной энергии mgh:

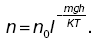
Такое распределение молекул в поле тяготения Земли можно качественно, в рамках молекулярно-кине-тических представлений, объяснить тем, что на молекулы оказывают влияние два противоположных фактора: гравитационное поле, под действием которого все молекулы притягиваются к Земле, и молеку-лярно-хаотическое движение, стремящееся равномерно разбросать молекулы по всему возможному объекту.

6. Математическая статистика и корреляционная зависимость

Математическая статистика – наука о математических методах систематизации и использования статистических данных для решения научных и практических задач. Математическая статистика тесно примыкает к теории вероятностей и базируется на ее понятиях. Однако главным в математической статистике является не распределение случайных величин, а анализ статистических данных и выяснение, какому распределению они соответствуют. Большая статистическая совокупность, из которой отбирается часть объектов для исследования, называется генеральной совокупностью, а множество объектов, собранных из нее, – выборочной совокупностью, или выборкой. Статистическое распределение – это совокупность вариант и соответствующих им частот (или относительных частот).

Для наглядности статистические распределения изображают графически в виде полигона и гистограммы.

Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (х₁; п₁), (х₂; п₂)…. или для полигона относительных частот – с координатами (х₁;р₁), (х₂;р₂)….

Гистограмма частот – совокупность смежных прямоугольников, построенных на одной прямой линии, основания прямоугольников одинаковы и равны а, а высоты равны отношению частоты (или относительной частоты) к а:

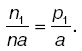
Наиболее распространенными характеристиками статистического распределения являются средние величины: мода, медиана и средняя арифметическая (или выборочная средняя). Мода (Мо) равна варианте, которой соответствует наибольшая частота. Медиана (Ме) равна варианте, которая расположена в середине статистического распределения. Она делит статистический (вариационный) ряд на две равные части. Выборочная средняя (ХВ) определяется как среднее арифметическое значение вариант статистического ряда.

Корреляционная зависимость. Функциональные зависимости можно выразить аналитически. Так, например, площадь круга зависит от радиуса (S = pr₂), ускорение F тела – от силы и массы (a = F/m₀). Однако имеются зависимости, которые не слишком очевидны и не выражаются простыми и однозначными формулами. Так, например, прослеживается связь между ростом людей и массой их тела, изменение погодных условий влияет на число простудных заболеваний населения и т. д. Такая более сложная, чем функциональная, вероятностная зависимость является корреляционной (или просто – корреляцией). В этом случае изменение одной их величин влияет на среднее значение другой. Предположим, что изучается связь между случайной величиной Х и случайной величиной Y Каждому конкретному значению Х будет соответствовать несколько значений Y: у₁, у₂ и т. д.

Условным средним Y_х назовем среднее арифметическое значение