Начертательная геометрия: конспект лекций

координатой х, при этом х = а?А (рис. 15), расстояние до фронтальной плоскости – координатой у, причем у = а?А, а расстояние до горизонтальной плоскости – координатой z, при этом z = aA.

На рисунке 15 точка А занимает ширину прямоугольного параллелепипеда, и измерения этого параллелепипеда соответствуют координатам этой точки, т. е., каждая из координат представлена на рисунке 15 четыре раза, т. е.:

х = а?А = Оа_х = а_уа = a_za?;

y = а?А = Оа_y = а_xа = а_zа?;

z = aA = Oa_z = а_xа? = а_yа?.

На эпюре (рис. 16) координаты х и z встречаются по три раза:

х = а_zа ?= Оа_x = а_yа,

z = а_xa? = Oa_z = а_yа?.

Все отрезки, которые соответствуют координате х (или z), являются параллельными между собой. Координата у два раза представлена осью, расположенной вертикально:

y = Оа_у = а_ха

и два раза – расположенной горизонтально:

у = Оа_у = а_zа?.

Данное различие появилось из-за того, что ось у присутствует на эпюре в двух различных положениях.

Следует учесть, что положение каждой проекции определяется на эпюре только двумя координатами, а именно:

1) горизонтальной – координатами х и у,

2) фронтальной – координатами x и z,

3) профильной – координатами у и z.

Используя координаты х, у и z, можно построить проекции точки на эпюре.

Если точка А задается координатами, их запись определяется так: А (х; у; z).

При построении проекций точки А нужно проверять выполняемость следующих условий:

1) горизонтальная и фронтальная проекции а и а? должны располагаться на одном перпендикуляре к оси х, так как имеют общую координату х;

2) фронтальная и профильная проекции а? и а? должны располагаться на одном перпендикуляре к оси z, так как имеют общую координату z;

3) горизонтальная проекция а так же удалена от оси х, как и профильная проекция а удалена от оси z, так как проекции а? и а? имеют общую координату у.

В случае, если точка лежит в любой из плоскостей проекций, то одна из ее координат равна нулю.

Когда точка лежит на оси проекций, две ее координаты равны нулю.

Если точка лежит в начале координат, все три ее координаты равны нулю.

Лекция № 3. Прямая

1. Проекции прямой

Для определения прямой необходимы две точки. Точку определяют две проекции на горизонтальную и фронтальную плоскости, т. е. прямая определяется с помощью проекций двух своих точек на горизонтальной и фронтальной плоскостях.

На рисунке 17 показаны проекции (а и a?, b и b?) двух точек А и В. С их помощью определяется положение некоторой прямой АВ. При соединении одноименных проекций этих точек (т. е. а и b, а? и b?) можно получить проекции аb и а?b? прямой АВ.

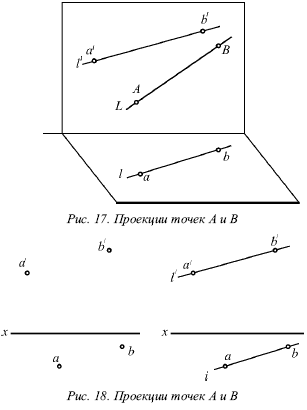
На рисунке 18 показаны проекции обеих точек, а на рисунке 19 – проекции проходящей через них прямой линии.

Если проекции прямой определяются проекциями двух ее точек, то они обозначаются двумя рядом поставленными латинскими буквами, соответствующими обозначениям проекций точек, взятых на прямой: со штрихами для обозначения фронтальной проекции прямой или без штрихов – для горизонтальной проекции.

Если рассматривать не отдельные точки прямой, а ее проекции в целом, то данные проекции обозначаются цифрами.

Если некоторая точка С лежит на прямой АВ, ее проекции с и с? находятся на одноименных проекциях прямой ab и а?b?. Данную ситуацию поясняет рисунок 19.

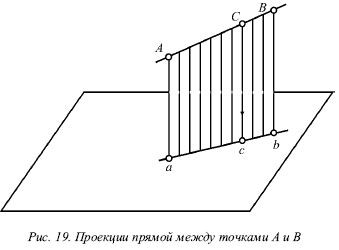
2. Следы прямой

След прямой – это точка пересечения ее с некоторой плоскостью или поверхностью (рис. 20).

Горизонтальным следом прямой называется некоторая точка H, в которой прямая встречается с горизонтальной плоскостью, а фронтальным – точка V, в которой данная прямая встречается с фронтальной плоскостью (рис. 20).

На рисунке 21а изображен горизонтальный след прямой, а ее фронтальный след, – на рисунке 21б.

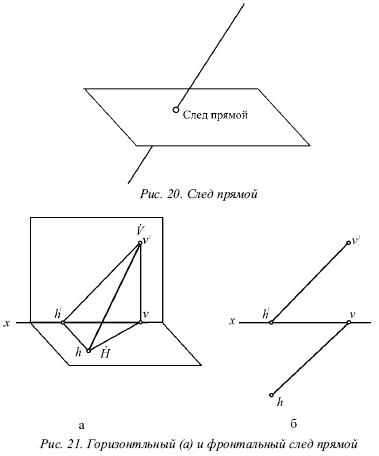
Иногда также рассматривается профильный след прямой, W – точка пересечения прямой с профильной плоскостью.

Горизонтальный след находится в горизонтальной плоскости, т. е. его горизонтальная проекция h совпадает с этим следом, а фронтальная h? лежит на оси х. Фронтальный след лежит во фронтальной плоскости, поэтому его фронтальная проекция ?? совпадает с ним же, а горизонтальная v лежит на оси х.

Итак, H = h, и V = ??. Следовательно, для обозначения следов прямой можно применять буквы h и ??.

3. Различные положения прямой

Прямую называют прямой общего положения, если она не параллельна и не перпендикулярна ни одной плоскости проекций. Проекции прямой общего положения тоже не параллельны и не перпендикулярны осям проекций.

Прямые, которые параллельны одной из плоскостей проекций (перпендикулярны одной из осей). На рисунке 22 показана прямая, которая параллельна горизонтальной плоскости (перпендикулярная оси z), – горизонтальная прямая; на рисунке 23 показана прямая, которая параллельна фронтальной плоскости (перпендикулярна оси у), – фронтальная прямая; на рисунке 24 показана прямая, которая параллельна профильной плоскости (перпендикулярна оси х), – профильная прямая. Несмотря на то что каждая из данных прямых образует с одной из осей прямой угол, они не пересекают ее, а только скрещиваются с нею.

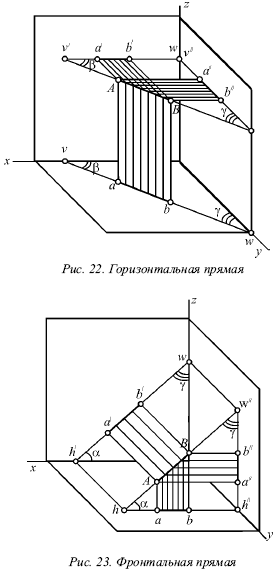
Из-за того что горизонтальная прямая (рис. 22) параллельна горизонтальной плоскости, ее фронтальная и профильная проекции будут параллельны осям, определяющим горизонтальную плоскость, т. е. осям х и у. Поэтому проекции a?b?|| х и a?b?|| у, т. е. они перпендикулярны оси z. Горизонтальная проекция ab может занимать любое положение на эпюре.

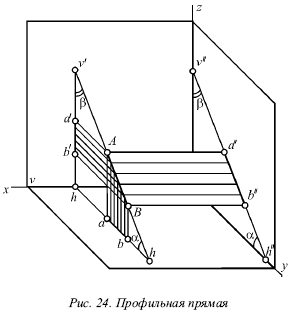
У фронтальной прямой (рис. 23) проекции аb