Физическая химия: конспект лекций

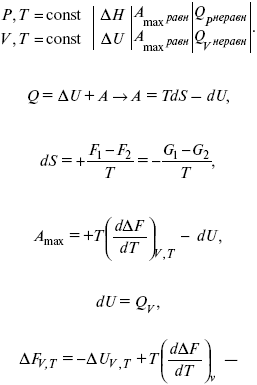
уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).

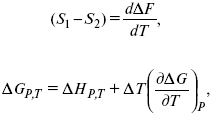
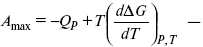
уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).

Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.

Уравнение Клаузиуса-Клапейрона

Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии

U₂ – U₁ = T(S₂ – S₁) – P (V₂ – V₁),

(U₁ – TS₁ + PV₁) = (U₂ – TS₂ + PV₂),

G₁ = G₂ – в условиях равновесия.

Предположим, что 1 моль вещества переходит из первой фазы во вторую.

I фаза => dG₁ = V₁dp – S₁dT.

II фаза => dG₂= V₂dp – S₂dT, при равновесии dG₂ – dG₁ = 0

dG₂ – dG₁ = dp(V₂ – V₁) – dT (S₂ – S1) –

нет условного равновесия,

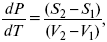
где dP/dT – температурный коэффициент давления,

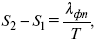
где ?_фп – теплота фазового перехода.

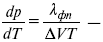
уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.

Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.

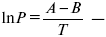
эмпирическая форма уравнения Клаузиуса-Клапейрона.

Рис. 7

Рис. 8

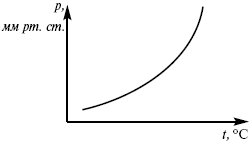
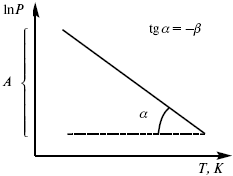
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.

I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.

II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.

I рода – ?G = 0, ?S ? 0, ?V ? 0.

II рода – ?G = 0, ?S = 0, ?V = 0.

Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.

Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).

Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Tи других свойств.

Итак, энтропия выражается уравнением:

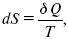
где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.

При независимых переменных U (внутренняя энергия) может обозначаться U_ВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:

1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;

2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, n_i;

3) внутренняя энергия при независимых переменных: S, V, n_i;

4) энтальпия при независимых переменных: S, Р, п_i;

5) энтропия при независимых переменных Н, Р, n_i..

В изолированных системах (U и V= const) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.

Связь энтропии с другими термодинамическими параметрами

Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = ?Q/T в сочетании с ?Q = dU + PdV и ?Q = dH – VdP дает уравнения:

dU = TdS – PdV,

dH = TdS + VdP.

Записав уравнение:

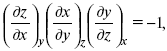
применительно к функциональной зависимости ?(Т, V, S) = 0, получим

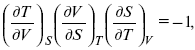
т. е.

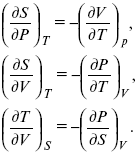
Теперь найдем зависимость энтропии от температуры из уравнений:

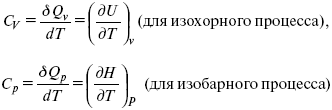
и

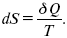
Вот эти зависимости:

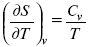
и

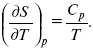
Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:

TdS = CdT.

Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.

Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.

Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.

Равновесие делится на устойчивое, неустойчивое и безразличное.

Постулаты второго закона термодинамики.

1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому