Регистрирующие понятия имеют конечный объем.
Общее понятие, относящееся к неопределенному числу элементов, называются нерегистрирующими. Напр., в понятиях «человек», «следователь», «указ» множество мыслимых в них элементов не поддается учету, в них мыслятся все люди, следователи, указы прошлого, настоящего и будущего. Нерегистрирующие понятия имеют бесконечный объем.
12. КЛАССИФИКАЦИЯ ПОНЯТИЙ ПО СОДЕРЖАНИЮ
По содержанию все понятия делятся на четыре группы.
• Положительные и отрицательные
Положительными называются понятия, содержание которых составляют свойства, присущие предмету. Напр., грамотный, порядок. Отрицательными называются понятия, содержание которых указывает на отсутствие у предмета определенных свойств. Напр., неграмотный, беспорядок. В русском языке такие понятия часто начинаются с приставок не– или без-. В словах иностранного происхождения с отрицательной приставкой – а-: анонимный, асимметрия. Необходимо отметить, что не все слова русского языка, начинающиеся на не– и без-, содержат отрицание признаков, напр. безделушка, негодование.
• Собирательные и несобирательные Собирательными называются понятия, в которых мыслятся признаки некоторой совокупности элементов, составляющих единое целое, напр. коллектив, полк, созвездие. Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в его объем, оно относится ко всей совокупности элементов. Напр., существенные признаки коллектива (группа лиц, объединенных общей работой, общими интересами) неприложимы к каждому отдельному члену коллектива. Собирательные понятия могут быть общими (коллектив, полк, созвездие) и единичными (коллектив нашего института, созвездие Большой Медведицы). Несобирательными называются понятия, в которых мыслятся признаки, относящиеся к каждому его элементу (звезда, государство, район). В процессе обсуждения общие понятия могут употребляться в разделительном и собирательном смысле. Напр., понятие «человек» в предложении «Человек осваивает космос» имеет собирательное значение, т. к. неприменимо к каждому человеку в отдельности, а в предложении «Человек имеет право на гражданство» имеет разделительное значение, т. к. относится к каждому человеку.
• Конкретные и абстрактные понятия
Конкретным называется понятие, в котором мыслится предмет или совокупность предметов как нечто самостоятельно существующее (книга, свидетель, государство). Конкретные понятия могут быть как общими, так и единичными. Абстрактным называется понятие, в котором мыслится признак предмета или отношение между предметами (смелость, ответственность, белизна, дружба, посредничество). Абстрактные понятия могут быть общими (посредничество, белизна) или единичными (гениальность Эйнштейна).
• Безотносительные и соотносительные понятия Безотносительными называются понятия, отражающие предметы, существующие раздельно и мыслящиеся вне их отношения с другими предметами (студент, государство, закон). Соотносительными называются понятия, содержащие признаки, указывающие на отношение одного понятия к другому (родители – дети, начальник – подчиненный, истец – ответчик). Знание видов понятий – одно из необходимых условий, обеспечивающих точность и ясность мышления. Чтобы оперировать понятием, необходимо не только четко знать его содержание и объем, но и уметь давать ему логическую характеристику. Напр., юрист – понятие общее (нерегистрирующее), несобирательное, конкретное, положительное, безотносительное.
13. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
По содержанию между понятиями могут быть только два вида отношений – сравнимость и несравнимость. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (романс и кирпич). Между ними невозможны логические отношения.
Сравнимые понятия – это понятия, имеющие в своем содержании общие, существенные признаки (по которым они и сравниваются). Напр., право и мораль. Отношения между понятиями изображают с помощью схем – кругов Эйлера. Между сравнимыми понятиями возможны два вида отношений по объему: совместимость и несовместимость.
Совместимые понятия – это такие, объемы которых полностью или частично совпадают. Между совместимыми понятиями складываются следующие отношения:
1 – равнообъемность. Равнообъемными или равнозначными называются понятия, которые различаются по своему содержанию, но объемы которых совпадают. Напр., «Л.Н. Толстой» – А и «автор романа «Война и мир» – В. Объемы тождественных понятий изображаются кругами, полностью совпадающими.
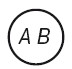
2 – перекрещивание. Перекрещивающимися называются понятия, объемы которых частично совпадают, напр. «студент» и «спортсмен», «юрист» и «писатель». Они изображаются пересекающимися кругами. В перекрещивающейся части двух кругов мыслятся студенты, являющиеся спортсменами. В левой части круга мыслятся студенты, не являющиеся спортсменами, а в правой части – спортсмены, не являющиеся студентами.
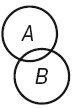
3 – подчинение. В отношении подчинения (субординации) находятся понятия, если объем одного полностью входит в объем другого, но не исчерпывает его. Это отношение вида – В и рода – А (млекопитающее и кошка).

Несовместимыми называются понятия, объемы которых не совпадают. Несовместимые понятия могут находиться между собой в следующих отношениях.
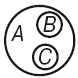
1 – соподчинение. В отношении соподчинения (координации) находятся понятия, объемы которых исключают друг друга, но принадлежат некоторому более общему родовому понятию. Напр., «ель» – B, «береза» – C принадлежат объему понятия «дерево» – А. Они изображаются неперекрещивающимися кругами внутри общего круга. Это виды одного и того же рода.
2 – противоположность. В отношении противоположности (контрарности) находятся два понятия, признаки которых противоречат друг другу, а сумма их объемов не исчерпывает родового понятия (храбрость – трусость).

3 – противоречие. В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя никакими другими (напр., А – белая краска, тогда понятие, находящееся с ним в отношениях противоречия, следует обозначить не-А (не белая краска). Круг Эйлера в этом случае делится пополам и между ними нет никакого третьего понятия.

14. ЛОГИЧЕСКАЯ ОПЕРАЦИЯ ОБОБЩЕНИЯ И ОГРАНИЧЕНИЯ ПОНЯТИЙ
Большое значение для достижения определенности нашего мышления имеют логические операции обобщения и ограничения понятий, основанные на законе обратного отношения между содержанием и объемом понятия.
Обобщить понятие – значит перейти от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом, но меньшим содержанием. Напр., обобщая понятие «городской суд», мы получим понятие «суд», объем нового понятия шире исходного, т. к. первое относится ко второму как вид к роду. Вместе с тем содержание нового понятия







