Но Асмодей не дает разгореться перепалке: он решительно возвращает филоматиков к разговору о кнопках, потому что спасение, по его словам, кроется именнов них.
— Задача, стало быть, состоит в том, чтобы нажать нужную, — соображает Фило. — Так ведь это же очень просто! Сколько их тут?
— У северной и южной дверей — по восьми, у восточной и западной — по четырнадцати, мсье.
— Итого сорок четыре. Не так уж много! Попробуем все — авось какая-нибудь да сработает.
— Вы меня не дослушали, мсье, — возражает черт, — а украинская поговорка недаром советует поперед батьки в пекло не лезть. Между прочим, в преисподней этот афоризм пользуется огромным успехом. Ко-ко!.. Так вот, да будет вам известно, что выбраться отсюда не так-то просто. Прежде всего из четырех дверей надо отобрать три, непременно соседние. Помимо того, у каждой из этих трех можно нажать только одну кнопку, причем двери эти также должны непременно следовать одна за другой — перескакивать через одну нельзя! А выйдем мы отсюда только в том случае, если из трех нажатых кнопок угаданы будут две, расположенные опять-таки у соседних дверей.
Фило безнадежно машет рукой. Ну и задачка! Попробуй тут угадай, с какой двери выгодней начинать…
— Зачем же гадать, мсье? Достаточно подумать.
— Ну, если так… Тогда, наверное, лучше начинать с той, где кнопок меньше.
— Это почему же? — интересуется Мате.
— Потому что там, где кнопок меньше, вероятность угадывания, естественно, больше. Кроме того, в этом случае двери с наименьшим числом кнопок нам встретятся дважды, а с наибольшим — только единожды. Логично или нелогично?
— Логично, но… неправильно.
Мате достает свой блокнот и вычерчивает круг с четырьмя дверьми.

— Допустим, мы начинаем с северной двери, где кнопок меньше, и угадываем нужную кнопку, но зато просчитываемся на следующей, восточной. Что нас ждет в этом случае?
— В этом случае сидеть нам здесь до второго пришествия, — мрачно острит Асмодей.
— Правильно. Если же начать с восточной или западной, где кнопок больше, то, даже просчитавшись на ней, мы все-таки можем угадать кнопки у двух последующих.
— Ха, ха и в третий раз ха! — выходит из себя Фило. — По-вашему, две трудные двери и одна полегче лучше, чем две полегче и одна трудная? Ну, знаете! Это еще надо доказать.
— И докажу!
Мате снова берет свой чертеж и начинает рассуждать.
— Как всегда, прибегнем к таблице и условимся передвигаться по часовой стрелке. Тогда у нас есть два варианта: СВЮ (мы начинаем с северной двери) и ВЮЗ (начинаем с восточной). В каждом из этих вариантов возможны только три благоприятных случая. Рассмотрим их, обозначив латинскими буквами а, b, с, а вероятности отгадывания — через p1 для варианта СВЮ и p2 для варианта ВЮЗ.
Итак, в обоих вариантах благоприятные случаи такие:
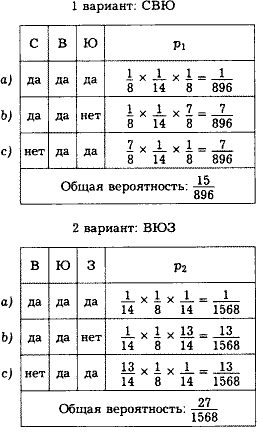
— Пока да. Но вот откуда в варианте
— Раз вы так наблюдательны, значит, должны были заметить, что 7/8 — это вероятность неугадывания. Ведь если вероятность угадывания равна 1/8, то вероятность неугадывания, естественно, равна 1 — 1/8, то есть 7/8. Ну а теперь нетрудно найти вероятность для всех трех случаев. Надо только сложить вероятности каждого.
— Позвольте, позвольте, — возражает Фило. — То вы перемножали, а теперь вдруг складываете…
— Что же вас смущает? Умножал я потому, что угадывания кнопок у каждой двери не зависят друг от друга и, стало быть, совместимы. Но ведь три случая — a, b и с не могут произойти одновременно. Значит, к ним применима теорема сложения, а не умножения вероятностей. Ну как? Теперь ясно? По лицу вижу, что ясно. В таком разе покончим с нашей задачей, вычислив общую вероятность для каждого варианта в отдельности: р1 = 15/896; р2 = 27/1568. Иначе говоря, р1 = 210/12544, а р2 = 216/12544. Так кто же был прав? Я или вы?
Фило обиженно таращится на таблицу. Пусть так! Прав Мате. Но не все ли равно, что стоит в числителе — 210 или 216 — при таком-то огромном знаменателе? Вероятность угадывания смехотворно мала и в том и в другом случае!
— Следовало ожидать, мсье, — говорит бес, небрежно помахивая тросточкой.
Фило так и подпрыгивает на своей подстилке!
— Вот как! — шипит он, дрожа от ярости. — Выходит, вы знали об этом заранее? Зачем же я как дурак решаю ваши идиотские задачи, если они все равно никаких дверей не откроют и к Монтальту меня не приведут?
— То есть как это — зачем? — притворно удивляется тот. — Конечно же для тренировки. Для усовершенствования вашего математического мышления.
— Не хочу мышления! — буйствует Фило. — Хочу к Монтальту! Хочу, чтобы открылись двери!
Асмодей оставляет наконец в покое свою тросточку и шумно вздыхает. Ничего не поделаешь! Если мсье так уж не терпится, двери, на худой конец, можно открыть и другим способом.
Он великолепным жестом достает из кармана большой позеленевший ключ, беззвучно вставляет его в замочную скважину…
И вот уже все они поднимаются сперва по узкой винтовой лестнице, а затем и в небо — в ясное, звездное, майское небо Парижа.
НАКОНЕЦ-ТО МОНТАЛЬТ!
— Ну знаете! — кипятится Фило, когда к нему возвращается дар речи. — Никогда не ожидал от вас ничего подобного! Ну зачем, зачем вам понадобилась вся эта комедия с подземельем, с запертыми дверьми и прочая и прочая?
— Кха, кха… Злосчастная страсть к театральным эффектам, мсье, — жалобно признается бес.
— Боюсь, что вы отстали от жизни. У нас, во второй половине двадцатого века, такие штучки давно вышли из моды. Мало того, их даже считают дурным тоном.
— Знаю, мсье, а поделать с собой ничего не могу. Старая школа! Так и тянет к неожиданным поворотам.
— Воображаю, что вы припасли для финала! — по обыкновению, язвит Мате.
— Для финала? — оживляется Асмодей. — Весьма кстати замечено, мсье. Спектакль-то идет к концу. Осталась одна-единственная картина.
— Не может быть! — искренне огорчаются филоматики.
— А Монтальт? Неужели мы так и не увидим Монтальта? — чуть не плачет Фило.
— Непременно увидите, мсье, — торжественно обещает бес. — Пароль донер! Честное асмодейское!

