Программирование на языке Пролог для искусственного интеллекта

Вопрос к системе — это всегда последовательность, состоящая из одной или нескольких целей. Для того, чтобы ответить на вопрос, система пытается достичь всех целей. Что значит достичь цели? Достичь цели — это значит показать, что утверждения, содержащиеся в вопросе, истинны в предположении, что все отношения программы истинны. Другими словами, достичь цели - это значит показать, что она логически следует из фактов и правил программы. Если вопрос содержит переменные, система должна к тому же найти конкретные объекты, которые (будучи подставленными вместо переменных) обеспечивают достижение цели. Найденные конкретизации сообщаются пользователю. Если для некоторой конкретизации система не в состоянии вывести цель из остальных предложений программы, то ее ответом на вопрос будет 'нет'.

Таким образом, подходящей интерпретацией пролог-программы в математических терминах будет следующая: пролог-система рассматривает факты и правила в качестве множества аксиом, а вопрос пользователя — как теорему; затем она пытается доказать эту теорему, т.е. показать, что ее можно логически вывести из аксиом.

Проиллюстрируем этот подход на классическом примере. Пусть имеются следующие аксиомы:

 Все люди смертны.

 Сократ — человек.

Теорема, логически вытекающая из этих двух аксиом:

 Сократ смертен.

Первую из вышеуказанных аксиом можно переписать так:

 Для всех X, если X — человек, то X смертен.

Соответственно наш пример можно перевести на Пролог следующим образом:

смертен( X) :- человек( X). % Все люди смертны
человек( сократ).           % Сократ - человек
?-  смертен( сократ).       % Сократ смертен?

yes                   (да)

Более сложный пример из программы о родственных отношениях, приведенной на рис. 1.8:

?- предок( том, пат)

Мы знаем, что родитель( боб, пат) — это факт. Используя этот факт и правило пр1, мы можем сделать вывод, что утверждение предок( боб, пат) истинно. Этот факт получен в результате вывода — его нельзя найти непосредственно в программе, но можно вывести, пользуясь содержащимися в ней фактами и правилами. Подобный шаг вывода можно коротко записать

родитель( боб, пат) ==> предок( боб, пат)

Эту запись можно прочитать так: из родитель( боб, пат) следует предок( боб, пат) на основании правила пр1. Далее, нам известен факт родитель( том, боб). На основании этого факта и выведенного факта предок( боб, пат) можно заключить, что, в силу правила пр2, наше целевое утверждение предок( том, пат) истинно. Весь процесс вывода, состоящий из двух шагов, можно записать так:

родитель(боб, пат) ==> предок( боб, пат)

родитель(том, боб) и   предок( боб, пат) ==>

 предок( том, пат)

Таким образом, мы показали, какой может быть последовательность шагов для достижения цели, т.е. для демонстрации истинности целевого утверждения. Назовем такую последовательность цепочкой доказательства. Однако мы еще не показали как пролог-система в действительности строит такую цепочку.

Пролог-система строит цепочку доказательства в порядке, обратном по отношению к тому, которым мы только что воспользовались. Вместо того, чтобы начинать с простых фактов, приведенных в программе, система начинает с целей и, применяя правила, подменяет текущие цели новыми, до тех пор, пока эти новые цели не окажутся простыми фактами. Если задан вопрос

?-  предок( том, пат).

система попытается достичь этой цели. Для того, чтобы это сделать, она пробует найти такое предложение в программе, из которого немедленно следует упомянутая цель. Очевидно, единственными подходящими для этого предложениями являются пр1 и пр2.

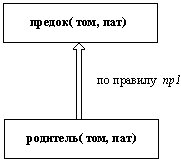
Рис. 1.9.  Первый шаг вычислений. Верхняя цель истинна, если истинна нижняя.

Это правила, входящие в отношение предок. Будем говорить, что головы этих правил сопоставимы с целью.

Два предложения пр1 и пр2 описывают два варианта продолжения рассуждений для пролог-системы. Вначале система пробует предложение, стоящее в программе первым:

предок( X, Z) :- родитель( X, Z).

Поскольку цель — предок( том, пат), значения переменным должны быть приписаны следующим образом:

X = том, Z = пат

Тогда исходная цель предок( том, пат) заменяется новой целью:

родитель( том, пат)

Такое действие по замене одной цели на другую на основании некоторого правила показано на рис. 1.9. В программе нет правила, голова которого была бы сопоставима с целью родитель(том, пат) , поэтому такая цель оказывается неуспешной. Теперь система делает возврат к исходной цели, чтобы попробовать второй вариант вывода цели верхнего уровня предок( том, пат). То есть, пробуется правило пр2:

предок( X, Z) :-
 родитель( X, Y),
 предок( Y, Z).

Как и раньше, переменным X и Z приписываются значения:

X = том, Z = пат

В этот момент переменной Y еще не приписано никакого значения. Верхняя цель предок( том, пат) заменяется двумя целями:

родитель( том, Y),
предок( Y, пат)

Этот шаг вычислений показан на рис. 1.10, который представляет развитие ситуации, изображенной на рис. 1.9.

Рис. 1.10. Продолжение процесса вычислений, показанного на рис. 1.9.

Имея теперь перед собой две цели, система пытается достичь их в том порядке, каком они записаны. Достичь первой из них легко, поскольку она соответствует факту из программы. Процесс установления соответствия — сопоставление (унификация) вызывает приписывание переменной Y значения боб. Тем самым достигается первая цель, а оставшаяся превращается в

предок( боб, пат)

Для достижения этой цели вновь применяется правило пр1. Заметим, — что это (второе) применение правила никак не связано с его первым применением. Поэтому система использует новое множество переменных правила всякий раз, как оно применяется. Чтобы указать это, мы переименуем переменные правила пр1 для нового его применения следующим образом: