name='105pt0pt1'>и
С'
разбиваются на капли. Эти капли падают в изолированные подставки
и
со вставленными воронками.
соединен проводником с
а
С'
с
Если
заряжен положительно, то образующиеся внутри
капли заряжаются отрицательно и отдают свой заряд
, заряжая тем самым
отрицательно. Из-за отрицательного заряда
образующиеся внутри него водяные капли получают положительный заряд и разряжаются в
увеличивая его положительный заряд. Заряды
,
и
возрастают до тех пор, пока изоляция препятствует проскакиванию искры».
Идея Кельвина изумительна по простоте и очевидности, и мы в своей лаборатории решили воплотить ее в реальных каплях и металлических бездонных цилиндрах и стаканах. Все, что изображено на рисунке, мы разместили под стеклянным колпаком, оградив от различных внешних воздействий, а от цилиндров С и
вывели из колпака проводники и присоединили их к двум одинаковым металлическим шарикам диаметром 1 см. Шарики укрепили на специальной подставке, и расстояние между ними сделали неизменным — 1 мм. Затем, открыв зажимы, дали возможность каплям падать и начали наблюдать: подсчитывали число упавших капель и следили, когда между шарами проскочит искра.
В тот момент, когда проскочила искра, между шариками была разность потенциалов 3000 вольт! Никто в наши дни не пользуется капельным методом, чтобы создавать высокие напряжения,— существуют способы помощнее... И все же нельзя не понять Эйнштейна, который был вос хищен кельвиновской идеей.
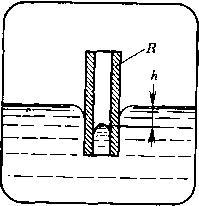
В мемориальной статье Эйнштейн рассказал еще об одной идее Кельвина, имеющей прямое отношение к капле. Кельвин заинтересовался следующим вопросом: как зависит давление пара жидкости вблизи поверхности от степени ее искривленности? Если рассуждать предметно, то речь идет о том, насколько отличается давление пара вблизи изогнутой поверхности водяной капли от давления пара вблизи плоской поверхности воды, налитой в широкое блюдце. В поисках ответа па этот вопрос Кельвин рассуждал так. Допустим, что в сосуд с жидкостью погружена тонкая трубка, внутренний радиус которой
R
.
Если жидкость не смачивает материал, из которого сделана трубка, то ее уровень в трубке расположится ниже, чем в широком сосуде, в который налита жидкость. Произойдет это по причине очевидной: в связи с тем что жидкость не смачивает стенок трубки, поверхность жидкости в ней будет выпуклой, полусферической, именно поэтому к жидкости будет приложено давление, направленное внутрь, то самое лапласовское давление, с которым мы уже встре чались, обсуждая опыт Плато. Под влиянием этого давлений уровень жидкости в трубке опустится ровно настолько, чтобы давление из-
sa
разности уровней жидкости в трубке и вне ее в точности равнялось лапласовскому. Его ве
личину мы
знаем:
л
= 2
α
/
Разность уровней
обусловит
давление
=
ρ
gh
.
Буквами обозначены следующие величины:
α
— поверхностное натяжение жидкости,
ρ
— ее плотность,
— ускорение силы тяжести. Приравняв два
эти давления, мы убедимся, что разница уровней
h
=
2α/
ρ
.
Таков результат первого этапа рассуждений Кельвина.
Второй этап — естественное продолжение первого. Над всей поверхностью жидкости — и той, которая в трубке, и той, которая в широком сосуде,— имеется пар этой жидкости, однако не везде давление, оказываемое им на жидкость, одинаково: несколько большим оно будет над по верхностью жидкости в трубке, так как слой пара над ней толще на величину
h
.
Очевидно, дополнительное давление этого слоя равно
Δ
=
ρ
0
gh,
где
ρ
— плотность газа, которая много меньше плотности жидкости. Величину
h
мы знаем — она была найдена на первом этапе рассуждений — и, следовательно, можем определить величину
Δ
Она очень важна, и поэтому формулу, которая определяет эту величину, мы вынесем на отдельную строку:
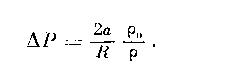
Вы читаете Капля

