двумя вершинами куба через центр, ее величина будет равна квадратному корню из трех. Кроме того, когда мы замеряем диаметры этих форм и их гармонические отношения, самым важным отношением будет конечно квадратный корень из пяти. Словами Лолора:
“Квадратный корень из пяти — соотношение, открывающее дорогу семейству соотношений, названному Золотым Соотношением[50] (или соотношением фи). Золотое Соотношение создает ряд символов, используемых философами-платониками для выражения идеала божественности или универсальной любви. Именно в свете Золотого Деления мы можем рассматривать тот факт, что Творец посадил возрождающееся семя, которое будет поднимать смертные сферы дуальности и беспорядка назад к образу Бога”.
Отсюда, связь квадратного корня из пяти с Платоновыми Телами выражается в том, что из нее непосредственно вырастает отношение фи. Сейчас, базируясь на работе Карла Мунка, мы видим, что Скорость Света также является непосредственной функцией квадратного корня из пяти. Более того, квадратный корень из пяти — функция Чисел Гематрии.
Это и есть тот самый краеугольный камень, который мы искали. Мы уже выявили гармоническую связь между “совершенными” гармоническими числами вибраций звука в воздухе. Эти “совершенные” числа появляются тогда, когда мы замеряем вибрации в секунду времени, которой пользуемся сейчас. Если бы наши секунды были короче, гармонические отношения все еще сохранялись бы, но больше не были бы целыми числами. Представляется, что секунда времени, пришедшая к нам от Шумеров, дает совершенно круглые числа вибраций каждой ноты Октавы. Одно только это указывает на высокий уровень научного знания, входившего в архаическую систему измерения. В последующих главах мы увидим: они сформулировали Большую Константу из Ниневии — число, позволяющее быстро вычислить орбиты всех планет, выраженные величиной в секундах.
Именно секунда, которой мы сейчас пользуемся, дает круглые и рациональные числа частот. Секунда времени — это точная гармоническая разбивка одного земного дня на 24 часа, где в каждом часе 60 минут, а в каждой минуте 60 секунд.
Мы знаем, что все числа Гематрии базируются на числе 9 как основе. Кэти показал: если мы переведем наши единицы времени с отношения 8 на отношение 9, в 27 “часов решетки”, то получим величину “секунд решетки”, демонстрирующую гармоническое “число частоты” 144 — Скорость Света в свободном пространстве. Также, мы видим, что “числа частоты” появляются более ясно при делении на число секунд Решетки в день.
Итак, короче говоря, сейчас у нас есть достаточно научных доказательств, чтобы утверждать: все Платоновы Тела, конечно, являются функцией математического расширения и сжатия изогнутых суперструн в сферическом энергетическом поле, создающих естественные формы. Например, одна из таких естественных форм, которую Хоагленд называет “строенным тором”, образуется при создании тетраэдра. Ту же информацию, касающуюся спиралевидных линий света, раскрыл Ра и другие источники; и сейчас мы наблюдаем это математически. Суперструны движутся со скоростью Света, и (из работы Кэти и Мунка) мы видим, что сами спирали являются функциями Света. Гармонические числа частоты, выраженные в Гематрии, тесно переплетены с “полотном” пространства и времени.
Итак, у нас есть пуленепробиваемый математический проект, объединяющий все различные положения воедино. Мы наблюдаем, как ЕС функционируют в своей “внутренней целостности” по их влияниям на энергетическое поле планеты. Как утверждал Ра, внутреннее расширение ЕС создает гравитацию. Сейчас, имея решетку Бэкера/Хэгенс, мы видим, что гравитация образно демонстрирует себя возникновением различных Платоновых форм. Реальные силовые линии, создаваемые этими формами, оказывают прямое воздействие на формирование континентальных масс суши.
Дальнейшая информация выявляется из прямой математической связи между Платоновыми геометриями и возникающими гармоническими числами. Как мы кратко упоминали, в конце конференции MUFON (1997) Ричард Хоагленд предложил закрытый предварительный просмотр фильма, демонстрирующего, что когда-то орбита Марса была длиной точно 666 марсианских дней, что является явно гармоническим числом. Мы уже знаем: когда-то в прошлом орбита Земли была точно 360 дней, и это могло бы послужить объяснением, почему мы используем для окружности 360 градусов. Поэтому, Эрол Торан решил посмотреть, что произойдет, если для окружности вместо 360-ти градусов будут использоваться 666. У команды Миссии Энтерпрайз имелся набор всех значимых угловых соотношений между различными сегментами тетраэдра, вписанного в сферу; за несколькими исключениями все они имели десятичные значения. Хоагленд открыл, что при использовании 666-ти градусов, все значения становятся целыми числами!
В нижеприведенной таблице мы показываем свои вычисления, основанные на предположении Хоагленда. Первая колонка показывает углы тетраэдра в 360-ти градусной системе, вторая указывает на то, что точную цифру следует гармонизировать с 666-ти градусной системой, третья дает величину в 666-ти градусной системе, четвертая выявляет, существует ли “гармоника” 666.
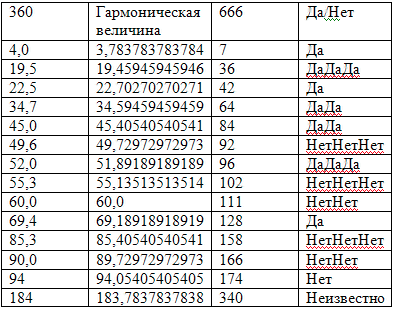
Из таблицы видно: чем больше “Да”, тем более гармонично число; и чем больше “Нет”, тем оно менее гармонично. Посмотрев на колонку Да/Нет, мы заметим: четко просматривается волновая форма. (Что касается последнего числа, информация о нем в гармонической таблице отсутствует, отсюда “Неизвестно”). Чтобы яснее видеть волновую форму, нам пришлось изобразить “Нет” в виде точек силы в противоположном направлении. Таким образом, очень интересно наблюдать: истинные гармоники формы тетраэдра представляются комбинацией очень гармонических и очень негармонических чисел. В случаях появления “Нет” лишь немногие числа делятся друг на друга, в случае многих “Да” числа гармонические, что означает наличие максимального числа множителей.
Рассматриваемая в совокупности, эта информация раскрывает огромную значимость. Сейчас у нас есть прочное математическое доказательство Миссии Энтерпрайз, связывающее углы одного из главных Платоновых Тел (почти определенно, что и других) с сериями гармонических чисел. Более того, особенно важно число “19,5”, представляющее самую значимую часть вписанного тетраэдра, ибо является точной гармоникой числа 36 — самого гармонического числа из всех. В “четырехэлементной” треугольной форме Пифагора существуют 36 рядов точек, начиная с одной точки на верху и кончая 36-ю точками внизу. Все вместе это формирует треугольник и представляет простую систему гармонического счета. Складывая все точки треугольника, мы приходим к тому же самому краеугольному “солнечному” числу 666.
Таким образом, в части 3, наблюдая гармонические числа, появляющиеся в Солнечной Системе, у нас будет больше оснований, чем прежде, видеть, что они напрямую связаны с Платоновыми геометриями. Представляется, что даже сама скорость света описывает гармоническую спираль, которую Кэти приравнял к 144 в гармонической системе времени, основанной на соотношении 9. Но, прежде чем перейти к заключительной части обсуждения, касающейся циклов времени, мы закончим экскурс в историю этого знания. Исследуя эффект “стекания” знания Атлантов в “секретные общества” прошлого и настоящего, можно проследить, как тщательно сохранялось все обсуждаемое нами знание.
Строчка за строчкой, посредством замечательного учения о “линиях лей”,[51] мы будем рассматривать, как древние народы охотились за энергиями Решетки; результаты такой охоты обнаруживаются по всей планете. Также, мы будем исследовать восхитительный виток истории, показывая, что и сейчас существует секретное общество, никогда не терявшее этого знания. Именно оно отвечало за формирование Правительства США и уделило внимание созданию Зала для Медитаций ООН. Мы продемонстрируем замечательное качество этого зала и предположим, что он является гиперпространственной “машиной”, построенной на принципах тщательно охраняемого секретного знания, которое постепенно становится доступным общественности.
Глава четырнадцатая: Великий Цикл, Глобальная Решетка и многомерная физика: историческая перспектива

