13. Метацентр и метацентрический радиус
Способность тела восстанавливать свое первоначальное равновесное состояние после прекращения внешнего воздействия называют остойчивостью.
По характеру действия различают статистическую и динамическую остойчивость.
Поскольку мы находимся в рамках гидростатики, то и разберемся со статистической остойчивостью.
Если образовавшийся после внешнего воздействия крен необратим, то остойчивость неустойчива.
В случае сохранения после прекращения внешнего воздействия, равновесие восстанавливается, то остойчивость устойчива.
Условием статистической остойчивости является плавание.
Если плавание подводное, то центр тяжести должен быть расположен ниже центра водоизмещения на оси плавания. Тогда тело будет плавать. Если надводное, то остойчивость зависит от того, на какой угол ? повернулось тело вокруг продольной оси.
При ? < 15o, после прекращения внешнего воздействия равновесие тела восстанавливается; если ? ? 15o, то крен необратим.
Точку пересечения архимедовой силы с осью плавания называют метацентром: при этом проходит также через центр давления.
Метацентрическим радиусом называют радиус окружности, частью которой является дуга, по которой центр давления перемещается в метацентр.
Приняты обозначения: метацентр – M, метацентрический радиус – ?м.
При ? < 15о

где I0 – центральный момент плоскости относительно продольной оси, заключенной в ватерлинии.
После введения понятия «метацентр» условия остойчивости несколько изменяются: выше говорили, что для устойчивой остойчивости центр тяжести должен находиться выше центра давления на оси плавания. Теперь предоложим, что центр тяжести не должен находиться выше метацентра. В противном случае силы и будут увеличивать крен.
Как очевидно, при крене расстояние ? между центром тяжести и центром давления меняется в пределах ?< ?м.

При этом расстояние между центром тяжести и метацентром называют метацентрической высотой, которая при условии (2) положительна. Чем больше метацентрическая высота, тем меньше вероятность крена плавающего тела. Наличие остойчивости относительно продольной оси плоскости, содержащей в себе ватерлинию, является необходимым и достаточным условием остойчивости относительно поперечной оси той же плоскости.
14. Методы определения движения жидкости
Гидростатика изучает жидкость в ее равновесном состоянии.
Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение.
Гидродинамика также изучает движение жидкости, но в зависимости от воздействия приложенных к жидкости сил.
В кинематике используется сплошная модель жидкости: некоторый ее континуум. Согласно гипотезе сплошности, рассматриваемый континуум – это жидкая частица, в которой беспрерывно движется огромное количество молекул; в ней нет ни разрывов, ни пустот.
Если в предыдущих вопросах, изучая гидростатику, за модель для изучения жидкости в равновесии взяли сплошную среду, то здесь на примере той же модели будут изучать жидкость в движении, изучая движение ее частиц.
Для описания движения частицы, а через нее и жидкости, существуют два способа.
1. Метод Лагранжа. Этот метод не используется при описании волновых функций. Суть метода в следующем: требуется описать движение каждой частицы.
Начальному моменту времени t0 соответствуют начальные координаты x0, y0, z0.
Однако к моменту t они уже другие. Как видно, речь идет о движении каждой частицы. Это движение можно считать определенным, если возможно указать для каждой частицы координаты x, y, z в произвольной момент времени t как непрерывные функции от x0, y0, z0.
x = x(x0, y0, z0, t)
y =y (x0, y0, z0, t)
z = z(x0, y0, z0, t) (1)
Переменные x0, y0, z0, t, называют переменными Лагранжа.
2. Метод определения движения частиц по Эйлеру. Движение жидкости в этом случае происходит в некоторой неподвижной области потока жидкости, в котором находятся частицы. В частицах произвольно выбираются точки. Момент времени t как параметр является заданным в каждом времени рассматриваемой области, которая имеет координаты x, y, z.
Рассматриваемая область, как уже известно, находится в пределах потока и неподвижна. Скорость частицы жидкости u в этой области в каждый момент времени t называется мгновенной местной скоростью.
Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается следующей системой:
ux = ux(x,y,z,t)
uy = uy(x,y,z,t)
uz = uz(x,y,z,t)
Переменные в (2) x, y, z, t называют переменными Эйлера.
15. Основные понятия, используемые в кинематике жидкости
Сутью вышеупомянутого поля скоростей являются векторные линии, которые часто называют линиями тока.
Линия тока – такая кривая линия, для любой точки которой в выбранный момент времени вектор местной скорости направлен по касательной (о нормальной составляющей скорости речь не идет, поскольку она равна нулю).

Формула (1) является дифференциальным уравнением линии тока в момент времени t. Следовательно, задав различные ti по полученным i, где i = 1,2, 3, …, можно построить линию тока: ею будет огибающая ломаной линии, состоящей из i.
Линии тока, как правило, не пересекаются в силу условия ? 0 или ? ?. Но все же, если эти условия нарушаются, то линии тока пересекаются: точку пересечения называют особой (или критической).
1. Неустановившееся движение, которое так называется иззза того, что местные скорости в рассматриваемых точках выбранной области по времени изменяются. Такое движение полностью описывается системой уравнений.
2. Установившееся движение: поскольку при таком движении местные скорости не зависят от времени и постоянны:
ux = ux(x,y,z)
uy = uy(x,y,z)
uz = uz(x,y,z)
Линии тока и траектории частиц совпадают, а дифференциальное уравнение для линии тока имеет вид:
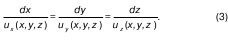
Совокупность всех линий тока, которые проходят через каждую точку контура потока, образует поверхность, которую называют трубкой тока. Внутри этой трубки движется заключенная в ней жидкость, которую называют струйкой.
Струйка считается элементарной, если рассматриваемый контур бесконечно мал, и конечной, если контур имеет конечную площадку.
Сечение струйки, которое нормально в каждой своей точке к линиям тока, называется живым сечением

