Философы Древней Греции

способом мы до сих пор изображаем числа на домино и игральных костях, а ассоциативная связь между числами и пространственными фигурами сохранилась в современных терминах «квадратные» и «кубические» числа. Фактически в течение всего Средневековья «фигурные числа» были стандартным крупнейшим разделом арифметики. Школьники заучивали теоремы о том, что, например, суммы последовательных целых чисел «треугольны», то есть составляющие их числа можно изобразить в виде треугольника (как в «тетрактисе десятки» на схеме, которая приведена ниже). Эта смесь воображения и абстракции позволяла легко ассоциировать числа с формами и предметами. Например, изображение чисел в виде группы единиц предполагало какую-то связь между единицами в арифметике и точками пифагорейской геометрии, и некоторые члены пифагорейской школы пытались построить физический мир из пространственных точек.

Для математика-пифагорейца числа не только продолжали нести в себе представление о физической форме и узоре, но имели и другие качества. У каждого числа были черты личности – оно могло быть мужским или женским, совершенным или несовершенным, красивым или уродливым. Современная математика постепенно избавилась от такого ощущения чисел, но его отголоски мы до сих пор находим в художественной литературе и поэзии. Самым лучшим числом было десять: оно содержало в себе четыре первых целых числа – один, два, три и четыре – и в точечной записи они образовывали совершенный треугольник. Списки чего-либо у пифагорейцев обычно делились на группы по четыре или по десять строк. Позже история чисел на Западе сложилась так, что математика пошла своим собственным путем, а идея личностных свойств и ценностных качеств чисел породила целую традицию в магии, нашедшую отражение в нумерологии и геомантике¹².

Поскольку математика пифагорейцев еще не достигла идеальной чистоты, они легко поверили в то, что «вещи – это числа». Интуитивное философское представление, выраженное этими словами, таково: определенная количественная форма вещи дает ей индивидуальность. Например, различные виды животных различаются между собой количеством и формой частей тела¹³. Уберите форму, и останется только лужа бесформенного вещества.

Математика и космология пифагорейцев

I. Фигурные числа

Чтобы показать, как каждое число складывается из монад, в пифагорейской системе «естественной» записи эти группы монад изображали с помощью маленьких букв альфа. Например, получались следующие соответствия:

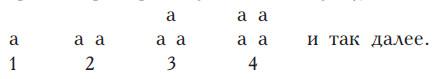
Изучение «фигурных чисел» развивалось по пути выяснения того, какую (в обобщенном виде) форму имеют числа, которые могут быть записаны в определенном виде. Например, произведения двух одинаковых сомножителей все были «квадратными». Суммы последовательных целых чисел, например, 1, 1+2, 1+2+3, 1+2+3+4 и так далее, имеют «треугольную» форму.

II. Тетрактис десятки

Фигурой, обладающей самыми чудесными свойствами, сочетающей в себе четыре первых целых числа, треугольную форму и «совершенное число» десять, был «тетрактис десятки» – треугольник из десяти монад, сложенный из целых чисел 1, 2, 3 и 4:

III. Таблица противоположностей

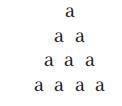
Как писал Аристотель, «некоторые пифагорейцы» для объяснения, как зародились числа и весь остальной мир, использовали таблицу противоположностей¹⁴.

Эту интерпретацию мы находим в ранней пифагорейской таблице противоположностей (которая приведена выше под номером III). В одном столбце – «формальные» качества, похожие на число или порождаемые числом; в другом собраны их противоположности, которые не имеют формы и становятся определенными только тогда, когда их ограничивают определением.

Другие представители пифагорейской школы толковали положение «вещи – это числа» более буквально. Поскольку выяснилось, что законы природы – количественные, было соблазнительно считать, что объекты, которыми эти законы управляют, тоже количественные. Если не брать в расчет иррациональные числа, то есть считать их исключением и отложить их исследование на потом, то аналогия между арифметической единицей и геометрической точкой подсказывала простую модель того, что вещи действительно были созданы из наборов точек. Каждый набор точек соответствовал фигуре, в которую складывались единицы, составлявшие одно из арифметических чисел.

Красота тезиса о том, что вещи – это числа, не только в его богатых возможностях для философии, но и в практических результатах, которые появились, когда ученые-пифагорейцы начали измерять и считать. По традиции считается, что Пифагор сам сделал открытие, которое привело к идее о «музыке сфер» – идее, гораздо позже вдохновлявшей людей науки и поэтов. Измеряя длину вибрирующей струны, которая производила гармоничные звуки, Пифагор обнаружил, что соотношения таких длин для октавы, пятой доли и четверти были точно 2:1, 3:2 и 4:3 – простейший из возможных набор соотношений целых чисел. А наблюдения показали с допустимой погрешностью, что в этих же самых соотношениях находились между собой периоды обращения планет. Таким образом, система небесных светил была гаммой, была гармонией, которая, как музыка, была математически простейшей¹⁵. (Некоторые энтузиасты понимали эту аналогию буквально, то есть считали, что каждая планета во время движения создает звук, высота которого пропорциональна скорости планеты. Но то, что сейчас называют космическим шумом, не слишком похоже на звучание всех семи нот музыкальной гаммы сразу.)

Это сходство гамм и звезд заставляло предполагать, что в природе все законы должны обладать такой же математической простотой. И пифагорейцы начали различными способами открывать, каковы эти лежащие в основе мира количественные соотношения. Для современной науки то, что изучение количественных данных помогает проникнуть в самую суть вещей, – урок, заученный наизусть, который она сейчас считает чем-то само собой разумеющимся. Но в те дни эта идея была новой, и можно себе представить, как волновались пифагорейцы, когда их метод в каких-то случаях имел успех, а в других терпел неудачу.

Пифагорейские идеи с самого начала успешно применялись в музыке и астрономии. По мере того как члены этой школы продолжали свои исследования, их новая методика, казалось, показала свою силу и в некоторых других областях знания. В медицине сицилийские врачи уже сформулировали определение здоровья как изономии – равновесия, или сбалансированности, в теле человека противоположных качеств – жары и холода, влаги и сухости¹⁶. Это представление очень близко по духу к пифагорейскому образу мыслей. И хотя я не видел ни одного исследования, специально посвященного этому вопросу, кажется несомненным, что медицина уже с первых попыток измерить температуру тела получила от этого пользу. Таким образом, пифагорейские идеи в сочетании с более ранними представлениями привели к созданию италийско-сицилийской медицинской теории, которая в греческой медицине была главной соперницей более эмпирического метода, созданного Гиппократом. В ваянии знаменитый скульптор Поликлет был одним из тех, кто верил, что красоту и правильность форм создают те же числовые соотношения, которые были обнаружены в музыке. Он полагал, что существует набор из «многих чисел», который описывает совершенные пропорции человеческой фигуры, и сам не только написал об этом исследование, но и создал согласно этим пропорциям статую, которая известна под названием «канон». В химии были высказаны будившие мысль смелые идеи о простоте геометрической формы мельчайших частиц материи. Важная роль правильных пропорций конечно же была центральной идеей греческой архитектуры. Казалось, не было границ способностями числа и пропорции проникать в самую глубину природы вещей, и именно эта их могучая сила поддерживала постоянный интерес к тезису «вещи – это числа» и делала его правдоподобным.

Помимо интеллектуального труда, Пифагорейское братство занималось еще тремя видами деятельности – политической, религиозной и этической. Эти остальные виды деятельности «ордена пифагорейцев» включали в себя переосмысление идей утопических общин, религиозные понятия об очищении, переселении душ в новые тела и каком-то виде бессмертия души, а также этическую идею о том, что жить хорошо – значит жить в гармонии с порядком, согласно которому устроен мир.

Политика всегда была одним из направлений деятельности этого братства. Идеалом Пифагора были