Красная земля, Черная земля. Древний Египет: легенды и факты

Долото и шило

Доказав, что слова «магия», «наука» и «религия» не имеют четко разграниченного содержания, мы начнем наше изучение египетской науки в той же самой критической манере – с утверждения, что науки, как таковой, в Древнем Египте не существовало. Египтяне были весьма искусны во многих практических ремеслах, для многих из которых требовалось использование научных законов, но эти законы формулировались редко – если вообще формулировались. Так же, как и в наши дни, египтяне вполне могли обойтись только технологией, обладая умением что-то делать и не интересуясь тем, почему оно получается как надо.

1. МАТЕМАТИКА

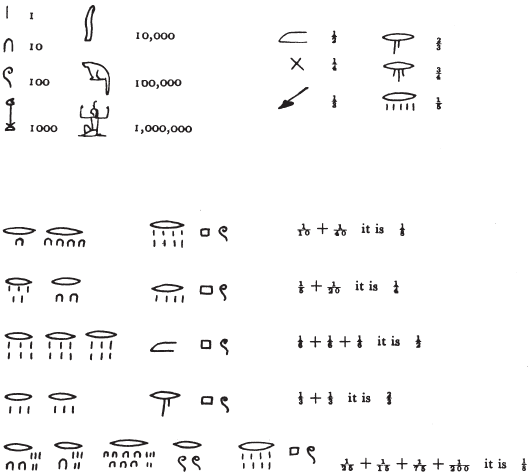
Вероятно, самой близкой к чистой науке в Древнем Египте была математика. Египтяне использовали десятичную систему, в которой единицу обозначала одна черточка. Двойкой были две черточки и так далее, вплоть до девяти. Для десятки существовал отдельный знак, похожий на ворота для крокета. Числа от одиннадцати до девятнадцати обозначались путем добавления к знаку десятки требуемого числа черточек. Число двадцать представляло собой двое «ворот для крокета», число двадцать один состояло из двух «ворот» и одной черточки. Помимо единицы и десяти, еще только несколько чисел имели собственные знаки – сто, тысяча, десять тысяч, сто тысяч и миллион. Для нуля знака не было.

Египетские числа

Египетская система составления чисел была еще более громоздкой, чем римская. Римляне могли записать число 1965 с помощью всего шести знаков. Египтянам для этого требовался двадцать один отдельный символ. На основе египетских цифр мы можем высказать предположение, что вычисление в Египте было утомительным занятием, и это предположение верно.

Очень похоже, что египтологи создали какие-то сложные, не дошедшие до наших дней науки. Если эти науки и были сложны, то они имели так мало значения, что о них не сохранилось ни единого свидетельства. В тех египетских науках, какие нам известны, успехи были совсем незначительными – хотя они и заслуживают определенного уважения, если помнить, что знания, на которых они основывались, были крайне скудны. Достижения египетской математики не более значительны, чем в других науках. Говоря по совести, даже математикой эту дисциплину назвать трудно, она представляла собой немногим больше, чем простая арифметика.

Их арифметика была арифметикой сложения по преимуществу. Даже умножение и деление проводили при помощи сложения. В качестве примера я хотела бы привести умножение восьми на шестнадцать – так, как это делали египтяне.

1 – 8

2 – 16

4 – 32

8 – 64

16 – 128

Все, что мы должны делать, – это удваивать каждую сторону таблицы, пока не получим требуемый ответ. Если у нас возникнет проблема, что такой процесс не дает четного результата, следует просто добавить два множителя, необходимых для получения требуемой суммы. Десять умножить на восемь, используя вышеприведенную таблицу, равно сумме восемь раз по восемь и два раза по восемь – шестьдесят четыре плюс шестнадцать, то есть восемьдесят.

Деление осуществляли таким же способом, только в обратном порядке. Для того чтобы разделить девяносто шесть на восемь, мы должны удваивать восемь (правая колонка вышеприведенной таблицы) до тех пор, пока мы не получим два числа, которые при сложении составят девяносто шесть. Этому требованию отвечает «тридцать два» и «шестьдесят четыре». Соответствующие им числа на левой стороне таблицы, которые мы, конечно, удваивали, как мы удвоили и правую колонку, – восемь и четыре. Восемь плюс четыре дают двенадцать. Это и есть правильный ответ.

Иногда метод удвоения не позволял получить полный ответ. Тринадцать, деленное на три, оказывается эквивалентно четырем тройкам с единицей в остатке. Как египтяне поступали с остатком?

Египетские дроби – вещь довольно интересная. Их обозначали словом «г» («часть»), которое ставили над числом. Слово «г» над числом «пять» обозначало одну пятую, «г» над воротами для крокета и четырьмя черточками было одной четырнадцатой и так далее. Как в иероглифическом письме, так и в иератическом, существовали отдельные знаки для одной второй, одной четвертой, двух третей, а также редко использовавшийся знак для трех четвертых. Но в обыкновенных подсчетах египтяне пользовались лишь дробями с единицей в числителе.

Но, скажет читатель, при таком ограничении осуществлять арифметические вычисления невозможно. Когда вы складываете или умножаете дроби – почти любые, – то получаете ответ, в котором числитель не является единицей. Египетский метод удвоения будет работать, только если числитель является четным числом. Дважды по одной четвертой равно двум четвертым, что сразу можно сократить, получив одну вторую. Дважды по одной третьей равны двум третьим, и у египтян был знак для этой дроби. Но удвоение одной пятой или одной седьмой дает результат, который египтяне не смогли бы выразить.

Однако они выражали. Но не в виде «двух пятых» или «двух седьмых». Вместо «двух пятых» они писали одну треть плюс одну пятнадцатую – что при сложении двух чисел дает тот же результат.

Конечно, подобная процедура довольно сложна, и писцу при подсчете дробей требовалось определенное время для того, чтобы правильно подсчитать каждую. Потому египтяне составили несколько таблиц, так что писцу уже не требовалось удваивать одну девятую – он просто смотрел в таблицу и находил в ней, что ответом является одна шестая плюс одна восемнадцатая. На нашей иллюстрации приведены исключения из подобного рода таблицы, показывающие путь решения при сложных дробях.

Специалист по догреческой науке профессор Отто Нойгебауэр писал, что «на практике умение использовать такие правила приходит очень быстро». Я уверена, что с ним так и было, но большинство из нас «оперировать» с египетскими дробями научились бы далеко не скоро! Нам будут мешать уже известные нам способы. Если бы мы с самого начала изучали египетскую арифметику, то, возможно, и сочли бы ее легкой.

Мы не можем точно знать, как египтяне использовали свои таблицы. Алгебры у них не было. Геометрия существовала; египтяне могли вычислять площадь треугольников, трапеций, прямоугольников и кругов, а также объем некоторых элементарных фигур, в том числе усеченной пирамиды. Вычисление объема усеченной пирамиды было самым впечатляющим достижением египетских математиков. Вызывает восхищение то, что египтяне считали число «пи» равным 3,16 – это довольно точное значение. Утверждают, что московский математический папирус описывает способ вычисления объема полушария, однако профессор Нойгебауэр полагает, что, скорее всего, папирус посвящен более простой задаче.

Математика – базовый инструмент наук – в Древнем Египте не только находилась в зачаточном состоянии, но и носила целиком прагматический характер. Дошедшие до нас математические тексты содержат таблицы и примеры решения задач, которые придворный или храмовый писец должен был уметь решать, – например, определить площадь поля или число кирпичей, необходимых для строительства сооружения с наклонной крышей заданных размеров. Греки мало что могли перенять из египетской математической мудрости – во многих отношениях вавилоняне ушли намного вперед от своих современников на юге.

2. АСТРОНОМИЯ

Египтяне имеют довольно высокую репутацию как астрономы; скорее всего, это связано с тем, что они создали хороший календарь, поскольку никакого другого существенного вклада в астрономию они не внесли. Их календарь – далекий предок нашего собственного, с его двенадцатью месяцами по тридцать дней в каждом и с пятью дополнительными днями, что в сумме составляет 365 дней. Известно, что астрономический год длился чуть дольше чем 365 дней, но прошло немало времени, пока человечество сообразило, как ему поступать с набегающей каждый год четвертью с небольшим суток. Египетский календарь эту добавку не учитывал, и в результате он скоро перестал соответствовать настоящему солнечному году. Тем не менее и такой календарь был значительным достижением по сравнению с лунным календарем других народов, в котором даже отдаленного совпадения с