папирусу вес даже больший, чем списку Манефона и данным Абидосской таблицы (см. [6], стр. 781— 782).
Четвертым основным документом древнеегипетской хронологии служит найденная Монетти близ Каира так называемая Таблица Саккара, в которой перечислено 58 египетских царей (см. ее копию в [6] на вклейке между стр. 782 и 783).
Казалось бы, что при таком обилии материала последовательный список египетских фараонов может быть установлен с большой надежностью. Но не тут–то было! Как мы увидим ниже, все источники, а не только восходящие к Манефону, сильно расходятся между собой, и задача их согласования затрудняет египтологов и по сей день. (Бикерман сообщает, что последняя заведомо не окончательная, реконструкция списка фараонов была произведена в 1945 г. (см. [12], стр. 100)).
Морозов заново исследовал все эти источники. Он опирался на Абидосскую таблицу, как на наиболее полную, но постоянно сравнивал ее со всеми другими данными. Так будем поступать и мы.
Абидосская таблица
Дадим слово самому Морозову:
«… что скажете вы по поводу следующего анекдота об Якове Бернулли, отце современной математической теории вероятностей.. ?
Когда Яков Бернулли был еще юношей и сидел, занимаясь в своей комнате в Базеле, пошел сильный град, который выбил стекло его окна, и на полу его комнаты оказалось 77 градин, расположившихся своеобразными группами. Он классифицировал их по их расстояниям от наружной стены и насчитал 15 групп, которые и отметил на полу меловыми линиями, параллельными стене. Стекло было вставлено в окно, но на следующий день пошел новый град, снова пробил стекло в окне и даже в другом месте, и, когда град кончился, он снова сосчитал попавшие к нему градины, и, к удивлению его, оказалось, что и теперь их лежит на полу тоже 77 градин и, можете себе вообразить? — они расположились между его меловыми линиями совершенно так же, как и прежние, только на месте предпоследней градины оказалось мокрое место, как будто бы она упала уже растаяв.
А в деталях вышло следующее.
Между его 1–й и 2–й линиями оказалось, при обоих случаях, как раз 8 градин, очень старого, особого вида, и первыми из них легли две крупные градины.
Между 2–й и 3–й линиями оказалось как раз 5 градин и в том и в другом случае, и вторая из них была тоже более крупной.
Между 3–й и 4–й линиями оказалось 7 градин и в том и в другом случае, и вторые две легли в каждом особо от других.
Между 5–й и 6–й линиями в первом случае оказались 4 такие огромные и своеобразные градины, каких он ни разу не видал в своей жизни, да и во втором случае оказались и такие огромные и своеобразные градины, каких он ни разу не видал в своей жизни…
И между всеми остальными его линиями получилось такое же точное числовое и даже качественное совпадение в обоих случаях, а последние градины у них были похожи на драгоценные камни, хотя оба града были независимы друг от друга, и пробоины в стеклах были различны. Это удивительное совпадение так заинтересовало молодого Якова Бернулли, что он принялся за изучение закона случайных совпадений и открыл свою знаменитую формулу в математической теории вероятностей…
— Позвольте! — прерываете вы, конечно, меня. — В тот момент, когда он открыл бы свою знаменитую формулу, он убедился бы, что оба эти града, или, по крайней мере, второй из них видел только во сне, так как сама же теория вероятностей показывает, что такого совпадения и по общему числу 77 и по отдельным группам в реальности не может быть. Даже если бы дело шло об одном и том же граде, падавшем в комнату через два одинаковых отверстия, то вероятность адекватного совпадения уменьшалась бы более, чем обратно пропорционально возрастанию числа упавших градин.
А здесь и обе пробоины независимы по своей величине и оба града независимы по своей продолжительности!… Это требует возведения 77 более чем в третью степень. А разделение градин на 15 одинаковых по качеству и количеству групп, причем в обоих случаях четвертая группа является исключительными градинами, которым равных не приходилось видеть в жизни, может быть только в волшебной сказке…
И вот эту–то самую волшебную сказку мы и видим в приложенной таблице (см. рис. 1 —
Скажите сами: не похоже ли это на сон? Для математика — это явное сновидение. Рассмотрим же эту ночную грезу в деталях» ([1], стр. 380—382).
Далее Морозов приводит список фараонов Абидосской таблицы (это и есть «родословная Рамзеса») в сопоставлении с родословной Иисуса по Евангелиям от Матфея и Луки. Мы опустим это, поскольку имена в обоих списках, как мы уже знаем, вполне «условны», а при замене их цифрами мы возвращаемся к рис. 1. Мы ограничимся тем, что приведем комментарии Морозова.
«I. Первые 8 царей Абидосской таблицы от Мены до Кебху выделены греческими авторами Евсевием, Африканом и другими в 1–ю (Тинитскую) династию и соответственно им первые 8 библейских патриархов (на левой стороне таблицы) представляют из себя особую группу, называемую допотопными патриархами, так сказать тоже «династия»…
Сравнение чисел предков Рэ–Мессу Миамуна в последовательных псевдодинастиях египетских царей по Абидосской таблице с числами предков Иисуса–Миссии в их естественных группах по Евангилею Луки (гл. 3).
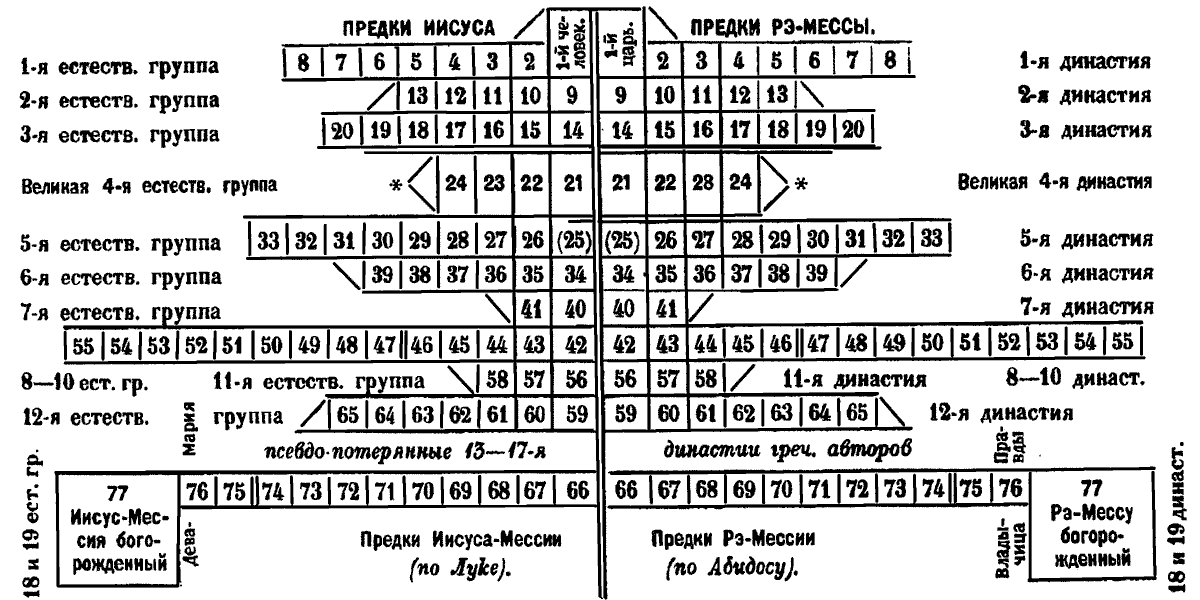
Параллелизм обеих сторон полный: каждый из 76 египетских предков Рэ–Мессы имеет своего изотопа в предках Иисуса–Мессии у Луки. Такое совпадение и общего числа, и отдельных групп возможно по теории вероятностей лишь в двух случаях:
1) если Рэ–Мессу тождественен с Иисусом–Мессией или
2) если это были два одновременные и различно знаменитые двоюродные брата.
Если же допустим, что все это миф, то — это тот же самый миф в двух разно–национальных ответвлениях.
Второй вывод: или библейские патриархи представляют из себя египетских царей под другими прозвищами, или наоборот. Другого выхода нет.
В ней первый египетский царь Мена соответствует первому библейскому патриарху Адаму. Если еврейское начертание имени Адам (АДМ) сравнить с иероглифическим начертанием Мены (МНА) и прочесть этот иероглиф (как допускается в египтологии) снизу вверх, то получим АДМ—АНМ, причем звук Н представляет, в сущности, звук Д с резонансом носовой полости.
II. Следующие 5 египетских царей… выделены теми же греческими авторами во 2–ю (Тинитскую же) династию, а в Библии их изотопы выделяются в естественную группу 5–ти послепотопных патриархов с присоединением к ним Ноева отца (Ламеха), и в иероглифе Ноя (точнее его аналога, фараона. —
III. Следующие 7 египетских царей выделяются египтологами в 3–ю (Мемфисскую) династию, а в Библии их изотопы выделяются в естественную группу потомков Евера…
IV. Следующие 4 египетские царя так своеобразно знамениты, как никакие другие в египетской истории, по великим пирамидам, воздвигнутым над ними. Первый из них Хуфу (или Хеопс греческих авторов)…;

