In the Land of Invented Languages

thoughtful and honest scholars must come to (whatever their life station) when their work reveals a vast, churning ocean of difficulty just beyond the charming rivulet they had glimpsed from afar.

The important insight of Lodwick’s system wasn’t in the symbols he chose (characters that look like capital letters, with various hooks, dots, and squiggles attached) but in the way his symbols expressed relationships between concepts. For example, as shown in figure 4.1, the symbol for “word,” , is the symbol for “to speak,” 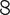, combined with a mark denoting “act of …”: . A word is essentially defined as an act of speaking. The symbol for God, 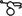, is the symbol for “to be,” 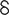, combined with “act of …,” , and “proper name,” . God is the proper name of the act of being (something like “The Embodiment of Existence”). The symbol for man, 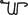, is the symbol for “to understand,” 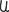, combined with “one who …,” , and “proper name,” . Man is “The Understander.” Lodwick’s major insight was to derive more complex concepts by adding together more basic ones.

Lodwick had hit upon the third method for creating a mathematics of discourse. It was concerned not with mere letters or numbers or symbols but with the relationships between the concepts they represented. From a limited set of basic concepts, you could derive everything else through combination. Leibniz would later describe this as a “calculus of thought.” The first rule of this calculus was that numbers for concepts “should be produced by multiplying together the symbolic numbers of the terms which compose the concept.” So, “since man is a rational animal, if the number of animal, a, is 2, and of rational, r, is 3, then the number of man, h, will be the same as ar: in this example, 2 ? 3, or 6.” The calculations work in reverse as well. If you saw that ape was 10, you could deduce that it was an animal (because it could be divided by 2) but not a rational one (as it can’t be divided by 3).

 

Figure 4.1: Lodwick’s symbols 

Descartes had also considered this idea a decade or two before Lodwick. He mused that if you could “explain correctly what are the simple ideas in the human imagination out of which all human thoughts are compounded … I would dare to hope for a universal language very easy to learn, to speak and to write.” But he never tried his hand at creating such a language, because he thought it would first require a complete understanding of the true nature of everything. While he did think it was “possible to invent such a language and to discover the science on which it depends,” he also thought this was unlikely to occur “outside of a fantasyland.”

Lodwick had hit upon a solution to the problem of how to make a mathematics of language, but the solution introduced a much bigger problem: How do we know what the basic units of meaning are? How do we define everything in terms of those units?

Well, you can start by figuring out the order of the universe. This was not a ridiculous proposition for the seventeenth-century man of science. It was a difficult proposition, and one that anyone could see would most likely never be adequately fulfilled. But that was no reason not to try. This was the age of reason, and so the rational animal got to work.

A Hierarchy of the Universe

The bulk of John Wilkins’s six-hundred-page description of his language is taken up with a hierarchical categorization of everything in the universe. Everything? When I first sat down to confront An Essay Towards a Real Character and a Philosophical Language, I did what any sensible, mature language scholar would do. I tried to look up the word for “shit.”

But where to look? I was holding a dictionary of concepts, not words. They were arranged not alphabetically but by meaning. To get the word for “shit,” I would have to find the concept of shit, which meant I had to figure out which of Wilkins’s forty categories of meaning it fell under.

Wilkins’s categories are organized into an overall structure of the type known as the Aristotelian hierarchy, or Porphyrian tree. This is the genus-species-difference organization we are most familiar with from taxonomies of plant and animal life. The higher positions in the tree are the most general categories, which are split into subcategories on the basis of some distinguishing feature. Daisies, spiders, woodpeckers, tigers, and porcupines all fall under the category of animate substances; they are all living things. But only some of them share the property of being sensate (bye, daisies) or of having blood (bye, spiders) or of being beasts (see ya, woodpeckers) or of being non-rapacious (so long, tigers). As we move down the tree, categories are narrowed and members more precisely defined by their membership.

Figure 5.1 shows Wilkins’s tree of the universe, with his forty numbered categories as the bottom nodes. The first division, general versus special, separates the big abstract metaphysical ideas (notions like existence, truth, and good) from the stuff of the world (the notions those ideas can apply to). This division was consistent with the philosophy of categories, descended from Plato and Aristotle, as practiced at the time. The division between substances and accident (at the second node under “special”) also comes from this tradition. Substances are answers to the question, What is this? and accidents are answers to the question, How/in what way/of what quality is this? A glance at the table will show that these distinctions do not always hold up very well, but, as Wilkins was quite aware, the philosophy was incomplete and this was as good a place to start as any.

The bottom nodes of this tree, the forty main categories, are themselves top-level categories in their own sprawling trees. For example, if we zoom in on category XVIII, “Beasts,” we find it further divided into six subcategories, as shown in figure 5.2.

It doesn’t stop there. Lift a subcategory and you find a tree of sub-subcategories that get even more specific. So under category XVIII (Beasts), subcategory V (oblong-headed), you will find six sub-subcategories under which specific animals are finally named (as shown in figure 5.3).

 

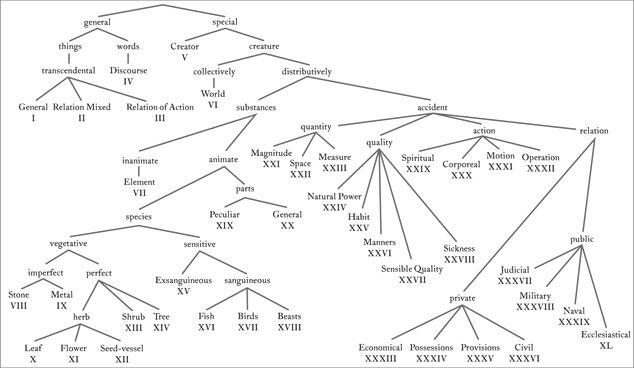
Figure 5.1: Wilkins’s tree of the universe 

 

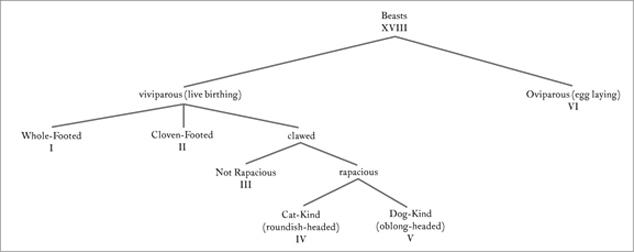
Figure 5.2: Subcategories of beasts 

 

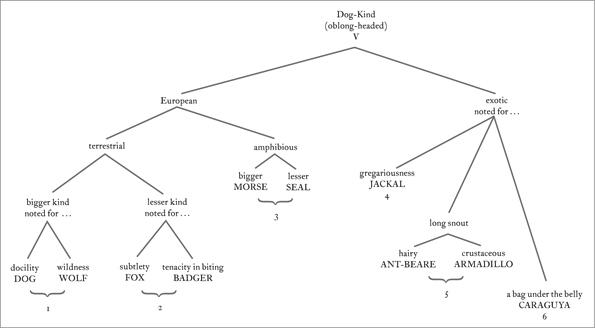
Figure 5.3: Subcategories of oblong-headed beasts 

Each one of his forty top-level categories expands in this manner into multiple sub- and sub-sub trees. A place is provided for everything from “porcupine” (substances > animate > sensate > sanguineous > beast > clawed > non-rapacious) to “dignity” (accident > quality > habit > instruments of virtue > concerning our conditions in relation to others) to “potentialness” (transcendentals > general > quality > degree of being). We are dealing with an enormous magnum opus here.

But why was all this necessary? What does the idea of a mathematics of language have to do with a gigantic conceptual map of the universe?

We have seen that a mathematics of language required two things: a list of the basic units of meaning, and a knowledge of how everything else was to be derived from those units. In Lodwick’s system “to understand,” “one who …,” and “proper name” were primitives, and “man” was derived from the combination of those three primitives. Man was defined as the one who understands. For Leibniz the primitives were rational and animal, and man was derived by the combination of those primitives—the rational animal. Well, which is it? Is man the rational animal or the understander? It depends on the primitives you’re working with. And finding the right set of primitives depends on finding the right definition. Now, the rational animal and the understander are pretty similar definitions for man—they both focus on man’s capacity to think—but man could be defined in other ways. Why not the upright-walking animal? Or (after Plato) the featherless biped?

Upright walking does not work, because, while it is a pretty distinguishing characteristic of man, it is not