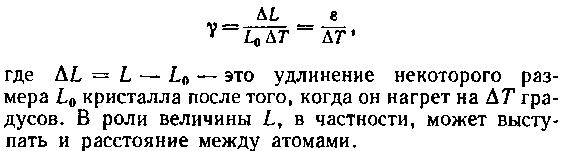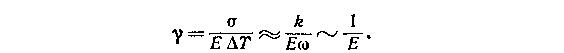По свежему следу предыдущего очерка воспользуемся моделью БНЛ для разговора о реальном взаимодействии между атомами, образующими кристалл.
Нам уже известно, что взаимодействие, т. е. конкуренция сил притяжения и отталкивания между атомами, обусловливает существование определенного расстояния l0 между ними. Уточним наше понимание «взаимодействия», проследив зависимость энергии этого взаимодействия W от расстояния l между атомами. Качественно ясно, что, если бы нам удалось атомы удалить друг от друга на бесконечное расстояние, энергия их взаимодействия стала бы равной нулю. Попросту говоря, бесконечно удаленные атомы друг о друге не осведомлены и поэтому между собой не взаимодействуют. Качественно ясно, что, как бы мы ни старались насильно сблизить соседние атомы, совместить их мы никогда не cможем, а это означает, что по мере уменьшения расстояния между атомами до нуля энергия отталкивания между ними должна стремиться к бесконечности. Собственно, при очень большом сжимающем давлении атомы могут «раздавливаться». Именно это и происходит, когда под давлением в миллионы атмосфер кристалл водорода металлизируется: раздавленные атомы водорода свой «личный» электрон отдают в коллективное пользование.
Качественно ясно также, что для того, чтобы исключить взаимодействие между соседними атомами, которые находятся на «равновесном» расстоянии l = l0, т. е. развести их на бесконечное расстояние, необходимо затратить вполне определенную энергию. Это означает, что при l = l0 энергия W = W0 будет отрицательной: именно она характеризует прочность связей в кристалле. Чем больше отрицательное значение W
0
, тем прочнее связи между атомами, тем большую энергию надо потратить для того, чтобы испарить кристалл. Так как испарить кристалл — это значит развести составляющие его атомы на бесконечность, то, очевидно, энергия W
0
и является мерой теплоты испарения.
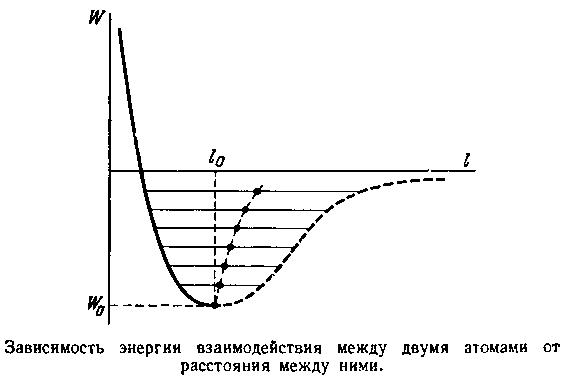
Вот теперь мы можем нарисовать кривую зависимости W от l. Передаваемый рисунком характер зависимости энергии взаимодействия между атомами от расстояния между ними физики называют «потенциалом взаимодействия». Он является фундаментальной характеристикой кристалла.
Продолжим извлекать следствия из факта существования определенного расстояния между атомами. Так как l0 и W0 — вполне определенные, конечные величины, а при удалении атомов их энергия взаимодействия принимает нулевое значение при l = ?, то кривая W (l) оказывается несимметричной относительно прямой, проходящей через точку l = l0. Очень важное следствие! Ведь оно означает, что с повышением температуры, когда тепловая энергия атомов возрастает, увеличивается не только амплитуда их колебаний, но и смещается в сторону больших значений l центр, вокруг которого эти колебания происходят, т. е. увеличивается «равновесное» расстояние между атомами. Попросту говоря, происходит тепловое расширение кристалла! На рисунке это обстоятельство изображено линией, которая проведена через середины отрезков, равных амплитудам колебаний атомов.
Здесь необходимо обратить внимание читателя на то, что и приведенные рассуждения, и иллюстрирующий их рисунок относятся к случаю, когда взаимодействуют лишь два атома, из которых один намертво закреплен в начале координат. В реальном кристалле все много сложнее: там и ближайших соседей несколько, и нет ни одного «начала координат». И все же приведенные рассуждения правильно передают физику обсуждаемых явлений. Заметьте: от простого факта существования кристалла логика естественно привела нас к необходимости его расширения с повышением температуры.
Коэффициент теплового линейного расширения ?, очевидно, должен быть связан с величинами, которые определяют и иные свойства и характеристики кристалла. Можно, например, ожидать, что чем прочнее связаны атомы в кристалле, т. е. чем больше модуль упругости E, тем меньше будет величина ?. Последнюю фразу следует воспринимать, разумеется, не как доказательство существования закономерности, а лишь как формулировку догадки о ней. А теперь попытаемся построже убедиться в существовании такой закономерности. Наших знаний теперь уже достаточно для того, чтобы вычислить коэффициент линейного расширения ?. Определяется он так:
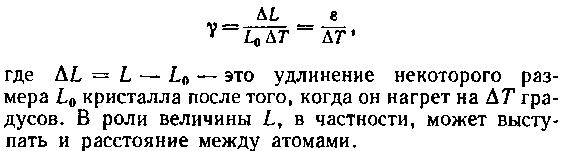
Относительное изменение расстояния между двумя атомами при нагреве кристалла подчиняется закону Гука, т. е. происходит под действием эффективного напряжения ? = ?E. Именно модуль упругости характеризует прочность связи атомов в кристалле: прочнее связь — больше модуль. Наша задача, таким образом, сводится к тому, чтобы понять происхождение и оценить величину ? и, следовательно, ?, а затем и ?.
Программа ясна, выполнить ее несложно. Когда мы нагреваем кристалл на ?Т градусов, каждый из его атомов получает дополнительную энергию теплового движения k ?Т. Здесь k — известная со школьной скамьи постоянная Больцмана. Если эта энергия расходуется лишь на то, чтобы увеличить расстояние между соседними атомами, то, видимо, рассуждать можно так. С одной стороны, дополнительная энергия равна k ?Т. С другой стороны, ее можно представить в виде произведения объема, приходящегося на один атом, ?, на то эффективное напряжение ?, действию которого атом подвержен. Строго я это доказывать здесь не стану, а только обращу внимание читателя на то, что если умножить объем, имеющий размерность см3, на напряжение, имеющее размерность эрг/см3, то получится эрг, т. е. действительно энергия. Итак, из условия k ?Т ? ?? следует, что ? ? k ?Т/?. Таким образом,
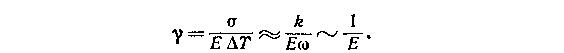
Дело сделано, действительно оказывается, что с ростом Е убывает ?. Так как для металлов Е ? 1012 эрг/см3, ? ? 3.10-23 см3, а постоянная Больцмана k = 1,38• 10-16 эрг/К, то ? ? 4• 10-6 К-1. Эта величина близка к той, которую можно найти в справочных таблицах.
Можно примыслить мудрого теоретика, который развил бы изложенную логику до наблюдения теплового расширения твердых тел и таким образом предсказал бы его. В действительности, однако, события развивались в обратном порядке. Тепловое расширение не могли не наблюдать еще первобытные, а их «теоретики» заведомо не были изощрены в потенциалах взаимодействия.
Оставим рассуждения в стороне и попробуем промоделировать взаимодействие между атомами. Весь ход зависимости энергии взаимодействия от расстояния между атомами моделировать сложно, а вот ту ее часть, которая соответствует притяжению между атомами и на предыдущем рисунке изображена пунктиром, мы промоделируем легко и просто, воспользовавшись моделью БНЛ.
Для нашего моделирования надо ухитриться создать на некотором расстоянии друг от друга всего два одинаковых мыльных пузырька. Удобно проводить опыт с пузырьками, диаметр которых 1—2 мм.