Разобщенные пузырьки без нашего вмешательства вначале очень медленно, а затем, ускоряясь, будут двигаться навстречу друг другу, пока не столкнутся. Столкнувшись, они соприкоснутся не в точке, а как бы вдавятся один в другой. Это хорошо видно на рисунке на с. 15.

Оказывается (именно так: оказывается!), что с изменением расстояния между пузырьками энергия их взаимодействия изменяется по закону, очень близкому к тому, которому подчиняются атомы в металлах. Следя за тем, как изменяется скорость сближения двух одинаковых пузырьков с уменьшением расстояния между ними, можно установить свойственный им ход зависимости
ОТКРЫТИЕ ДЮЛОНГА И ПТИ
В истории физики 1819 г. отмечен свершением: французские ученые Пьер Луи Дюлонг и Алексис Терез Пти опубликовали результаты своих опытов по измерению теплоемкости твердых тел. Обобщая эти результаты, они сформулировали фундаментальный закон, согласно которому произведение теплоемкости одного грамма вещества в твердом состоянии на его молярную массу есть величина почти одинаковая для всех веществ, не зависит от температуры и составляет около шести калорий. Или, по-иному, теплоемкость в расчете на моль для всех веществ одна и та же: 6 кал/(моль•К). Осторожные слова «почти» и «около» нисколько не умаляют значимости обобщения. Это будет ясно из дальнейшего.
Сейчас трудно надежно реконструировать психологическую канву, на фоне которой было сделано это открытие, но думается, что, найдя такое широкое обобщение, Дюлонг и Пти должны были быть потрясены его величием. Так как моль любого вещества содержит одно и то же количество атомов, то находка Дюлонга и Пти означает, что для повышения на один градус температуры твердого вещества каждый его атом поглощает одно и то же количество энергии. Ничего удивительного нет в том, что все атомы данного элемента равноправны: с чего бы, собственно, им отличаться? А вот что перед законом равны и атомы различных элементов — это должно было бы поразить и открывателей, и их современников.
Для нас, прослеживающих судьбы живого кристалла, закон Дюлонга и Пти может явиться источником сведений о том, как движутся атомы в кристалле, — именно поэтому и начат рассказ о теплоемкости. Ведь тепло, поглощаемое кристаллом при его нагреве, расходуется на увеличение интенсивности теплового движения атомов.
Сделаем конкретное предположение о характере этого движения и попытаемся теоретически оправдать закон Дюлонга и Пти. Можно было бы строить логику в обратном порядке: исходить из закона Дюлонга и Пти и пытаться понять, какому характеру движения атомов он соответствует. Воспользуемся первой возможностью.
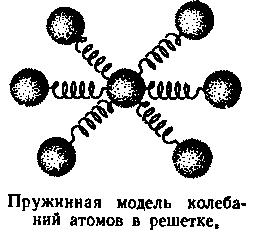
Допустим, что каждый атом в узле кристаллической решетки колеблется подобно маятнику независимо от своих соседей, ближних и тем более дальних. Воспользуемся следующей моделью кристалла и происходящего в нем теплового движения. Представим себе атом в виде весомого шарика, укрепленного на трех парах взаимно перпендикулярных пружинок так, как это изображено на рисунке. Три пары пружинок символизируют то обстоятельство, что атом может колебаться в трех взаимно перпендикулярных направлениях. Физики говорят так: атом имеет три независимые степени свободы. Итак, принимаем модель: кристалл — совокупность упорядоченно расположенных в пространстве «трехпружинных» маятников, каждый из которых по существу является совокупностью трех осцилляторов.
Прежде чем эту модель положить в основу расчета теплоемкости, необходимо определить энергию колеблющегося маятника. Безотносительно к значению этой энергии можно утверждать, что в течение одного периода колебаний маятника ее величина должна оставаться неизменной, к этому ее обязывает закон сохранения энергии. В предыдущей фразе упомянут «один период» лишь потому, что любой из периодов в равной мере подвластен закону сохранения энергии. В колеблющемся маятнике последовательно происходит преобразование кинетической энергии в потенциальную и потенциальной в кинетическую, при этом в среднем за период каждая из этих энергий оказывается равной
В кристалле, масса которого равна молярной, имеется
Серьезный успех: мы придумали элементарную модель теплового движения в кристалле и получили закон Дюлонга и Пти. Прочтем наш результат немного по-иному: согласующийся с нашим расчетом и экспериментально подтвержденный закон Дюлонга и Пти свидетельствует о том, что мы, видимо, правильно понимаем характер теплового движения атомов в кристалле, воплощенный в нашей модели.

Все сказанное — правда, однако не вся правда. Хочется сказать так: только «высокотемпературная» часть правды. Дело в том, что прошло не более десяти лет после открытия Дюлонга и Пти, как было обнаружено, что некоторые тугоплавкие вещества, например алмаз, не подчиняются этому закону. А потом было установлено, что теплоемкость таких веществ не является постоянной, как это предсказывает закон Дюлонга и Пти, а увеличивается с ростом температуры, стремясь к тому значению, которое законом предусматривается.
Со временем, когда научились экспериментировать в области низких температур, выяснилось, что особенность поведения тугоплавких веществ — никакая не особенность, а, наоборот, является нормой для всех веществ.
Эта «особенность» впервые обнаружилась на тугоплавких веществах просто потому, что «комнатная» температура по сравнению с их температурой плавления низка. Закон Дюлонга и Пти, обнаружившись, выглядел откровением, а на поверку оказался лишь долей правды, ее «высокотемпературной» частью!
Отвлечемся от того чувства разочарования, которое, видимо, испытывал Дюлонг (Пти ушел из жизни вскоре после открытия закона). Закроем пока глаза на «низкотемпературную» правду и тщательнее вдумаемся в открытие французских физиков: «низкотемпературная» правда не отменяет справедливости закона Дюлонга и Пти в области высоких температур, где закон может быть использован для уточнения характеристик теплового движения атомов.
Из закона Дюлонга и Пти, разумеется применительно к той области температур, где он

