Живой кристалл

подтверждается экспериментально, следует, что, участвуя в тепловом движении, атомы в узлах решетки колеблются подобно обычным маятникам. До сих пор мы довольствовались лишь знанием энергии этих колебаний. А теперь построим элементарную теорию колебаний атома в кристалле и установим амплитуду А и период ?₀ этих колебаний.

Немного упростим модель кристалла. Пусть атомы, окружающие данный «одиночный» атом, колебаний не совершают, а лишь, взаимодействуя с колеблющимся, определяют силы притяжения и отталкивания, которые действуют на него в соответствии с потенциалом взаимодействия между ним и окружающими атомами. И еще больше упростим реальную ситуацию, допустив, что атом совершает колебания лишь вдоль определенной прямой, а не во всех трех направлениях в пространстве. В рамках такой модели естественно атом, колеблющийся в узле решетки, мысленно заменить грузиком, колеблющимся на пружинке: грузик — атом, пружинка — упругое окружение. К помощи пружинки мы недавно уже прибегали.

Не увели ли нас предположения и упрощения далеко в сторону от тех реальных условий, в которых колеблется реальный атом в узле реальной кристаллической решетки? Кажется, не увели. Пружинка удачно моделирует наличие силы притяжения (когда она растянута) и силы отталкивания (когда она сжата). Грузик хорошо моделирует атом, так как в нашей задаче, если силы заданы, от атома требуется лишь иметь определенную массу, а грузик ее имеет. А то, что в избранной модели колебания происходят вдоль прямой, существа дела практически не искажает, так как более сложное колебание можно представить в виде суммы прямолинейных, — этой возможностью мы уже пользовались, когда, объясняя открытие Дюлонга и Пти, предполагали, что каждый из атомов участвует в трех прямолинейных колебаниях.

Определим вначале амплитуду колебаний атома. Потенциальная энергия W_п колеблющегося грузика, очевидно, не должна зависеть от того, смещается он влево или вправо от своего среднего положения, когда пружина и не сжата, и не растянута. А это означает, что

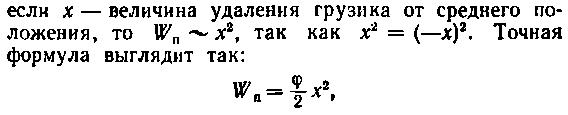
где ? — постоянная величина, характеризующая упругие свойства пружины. Эта величина определяет силу, действующую на грузик со стороны пружины: F = — ?х.

При максимальном отклонении колеблющегося атома от положения равновесия, т. е. при отклонении на величину амплитуды колебаний А, как мы уже знаем, вся энергия атома kТ будет запасена в виде потенциальной энергии. Это означает, что

?A²/ 2 = kT

и, следовательно,

A = (2kT / ?)^1/2

Полученная формула неприятна тем, что в нее входит неизвестная нам величина ?. Впрочем, ее нетрудно связать с известными характеристиками кристалла. Для этого левую и правую части формулы, которая определяет силу F, поделим на а², где а — межатомное расстояние:

F/а² = - ?/а ^. x/а

Легко усмотреть, что F/a² — напряжение, действующее на атом, х/а — относительное смещение атома. Если оно невелико, последняя формула просто является записью закона Гука, а отношение ?/а имеет смысл модуля упругости Е. Итак, ? = Еа , а амплитуда

A = (2kT/Ea) ^1/2 ? T^1/2

Из нашего расчета следует, что амплитуда колебаний атома с температурой возрастает по закону T^1/2. У металлов, для которых Е ? 10¹² дин/см², а ? 3• 10^-8 см, в области предплавильных температур амплитуда А ? 2^.10^-9 см и, следовательно, составляет несколько процентов от величины межатомного расстояния. Много это или мало? Конечно же, немного, если иметь в виду сохранение решетки как таковой, если заботиться о том, чтобы тепловые колебания не расшатали кристалл, лишив его порядка в расположении атомов. При найденной нами амплитуде колебаний атомов кристалл сохраняет свою индивидуальность, еще не теряет «черты кристалла».

Определим теперь период колебаний атома. Если иметь в виду лишь приближенную оценку, то сделать это совсем несложно. Когда вся тепловая энергия колеблющегося атома преобразована в его кинетическую энергию, атом движется с максимальной скоростью, которая следует из условия

Мы сделали грубое предположение, сочтя, что на протяжении всего периода колебаний атом движется с максимальной скоростью. Как выясняется, оно привело нас к потере численного множителя 2?. Точная формула выглядит так:

  

Мы получили результат, противоречащий интуиции: кажется странным, что период колебаний атома в решетке практически не зависит от температуры, разве что лишь в меру очень слабой температурной зависимости модуля упругости. Здесь следует подчеркнуть: не при всех температурах, а лишь при высоких температурах, когда вообще справедливо все то, что рассказано в очерке. Так как масса атома  

m ? 10^-22 грамм, то ?₀ = 10^-13 - 10^-12 с 

Итак, мы оценили две фундаментальные характеристики движения атома в кристалле: амплитуду и период колебаний. Их значения свидетельствуют об очень активной жизнедеятельности атома: он за секунду, не меняя положения оседлости, совершает п = 1/?₀ = 10¹² — 10¹³ колебаний, проходя при этом путь протяженностью L = па = (10¹² — 10¹³)• 10^-9 см = 10³ — 10⁴ см!

История закона Дюлонга и Пти — отличная иллюстрация к одной из общих закономерностей развития науки: в ее ткань входят не только завершенные «глыбы» правды, но и те «крупицы» знаний, которые оказываются лишь долей правды.

ТЕОРИИ ЭЙНШТЕЙНА И ДЕБАЯ