Капля

несом.

 

Теперь о следствиях нового прочтения формулы. И не

о  всех, а о самом главном, ради которого стоило присталь­но всмотреться в старую формулу и заново ее прочесть.

 

Перенос жидкости из капли в блюдце

 

Капля пустоты (пора) испаряется в кристалл. Вблизи поры много вакансий (зачерненные кружки), вдали — мало

Вот опыт, который демонстрируют на школьных уро­ках физики или рассказывают о нем. Небольшой стеклян­ный колпак (перевернутый стакан) установлен на стек­ле. Под колпаком блюдечко с водой и рядом на предмет­ном стеклышке капли воды. Эти капли надо поместить на стеклышко после того, как пространство под колпаком на­сытится водяным паром, который образуется над пло

ской поверхностью воды в блюдце. Через некоторое время капли исчезнут — они испарятся, а возникшие при этом в водяном паре молекулы воды сконденсируются на по­верхности воды в блюдце.

Итак, в начале опыта под колпаком было три объекта: вода в блюдце, вода в каплях и насыщенный водяной пар. Опыт окончился, когда один из объектов исчез — капель не стало. Здесь все ясно: согласно формуле, давление пара над изогнутой поверхностью водяной капли больше, чем над плоской поверхностью воды в блюдце, и пар под влиянием этой разности давлений двигался по направлению к блюд­цу — уходил оттуда, где его давление больше, и приходил туда, где его давление меньше. Чтобы вблизи своей поверх­ности поддерживать давление, предписываемое ей форму­лой, капля должна все время испаряться. Она это добро­совестно делала и в конце концов исчезла.

А теперь тот же опыт только не с каплями и атомами ре­альной жидкости, а с «каплями» и «атомами» пустоты. Вме­сто колпака с блюдцем и каплей — монокристалл. Он огра­нен плоскими поверхностями и в объеме имеет одну пору сферической формы. Вблизи изогнутой поверхности поры (капля!) концентрация вакансий повышена, а вблизи плоской поверхности, которая отделяет кристалл от ок­ружающего пространства (вода в блюдце!), концентрация вакансий нормальная, не повышена. Очевидно, появится поток вакансий от поры к поверхности кристалла, и, подобно капле воды, пора исчезнет — «испарится в кри­сталл». Образовавшийся при этом в кристалле избыток вакансий со временем сгладится — вакансии либо по­глотятся внутренними стоками, либо с помощью диффузии переместятся к внешней поверхности кристалла.

Начали мы опыт с пористым, а окончили с беспористым кристаллом! Как быстро это произойдет? Все зависит от размеров поры и температуры кристалла. Например, пора, радиус которой один микрон, в медном кристалле при тем­пературе 1000° С исчезает приблизительно за 30 мин.

Все рассказанное о формуле, об аналогии между реаль­ными каплями и каплями пустоты лежит в основе целого раздела современной физики твердого тела— физики спе­кания, которая объясняет, как пористые кристаллические тела самопроизвольно при высоких температурах превра­щаются в плотные. Оказывается, капли пустоты могут испаряться в кристалл!

Удобная «постель» для капли

В названии очерка нет надуманности — его содержание находится в полном соответствии с названием. Дело в том, что гладкая, чистая, полированная поверхность твердого тела для жидкой капли неудобна. Попав на нее, капля бу­дет пытаться изменить, улучшить подложку, сделать ее более удобной, даже если для этого ей придется трудиться очень долго.

 

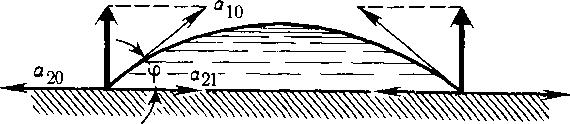
Взаимное расположение сил, действующих на контур капли, лежащей на гладкой твердой поверхности

Напомню, что нет ничего удобнее для капли, чем быть взвешенной в пространстве, в невесомости: ни с чем она не соприкасается, никакие силы ее не искажают и ни к ка­ким изменениям она не стремится. А на пластинке с пло­ской поверхностью все не так, даже если пластинка с кап­лей находится в невесомости.

Вначале подумаем над тем, чем гладкая поверхность не­удобна для жидкой капли. Казалось бы, капля подвижна и должна, переливаясь, как-то приспособиться к плоской поверхности, сделать свое пребывание на ней удобным. Оказывается, что одним изменением собственной формы добиться этого капля не может.

Посмотрите на приведенный рисунок. На нем изображе­на капля жидкости, смачивающей твердую поверхность (угол φ — острый). Стрелками обозначены силы, обуслов­ленные поверхностным натяжением на границе подлож­ка — капля (α₂₁), подложка — воздух (α₂₀) и капля — воздух (α₁₀). Все дальнейшее можно было бы рассказать, имея в виду и каплю, не смачивающую твердую поверх­ность. Но мы остановимся на случае, который изображен на рисунке. Из него с очевидностью следует, что три силы, которые соответствуют поверхностным натяжениям твер­дое — воздух, твердое — капля и капля — воздух, ни при какой форме капли не могут прийти в равновесие, так как первые две из них направлены одна против другой и лежат в одной плоскости, а третья — под углом к ней. Именно поэтому имеется нескомпенсированная сила, приложенная к контуру капли,— на рисунке она обозначена жирной стрелкой и, пожалуй, может считаться количественной мерой степени неудобства подложки. Капле надо сделать что-либо с собой или с подложкой, чтобы избавиться от нее.

Можно рассказать об этом по-другому. Выпуклая по­верхность капли создает давление, которое прижимает ее к плоскости. Это так называемое капиллярное (лапласовское) давление — мы уже с ним встречались. Участок же поверхности капли, который граничит с твердой под­ложкой, такого давления не создает: оно должно быть пропорциональным 1/

R

, а радиус кривизны плоского участка

поверхности капли равен бесконечности, и, значит, давле­ние равно нулю. К одному участку поверхности давление приложено, к другому — не приложено, а это неудобно. Капля, подвешенная в невесомости, таких неудобств не испытывает.

Два разных рассказа об одном и том же явлении можно проиллюстрировать двумя опытами. Опыт первый иллю­стрирует первый рассказ, опыт второй — второй.

Опыт первый. На полированной поверхности стеклян­ной пластинки, сухой и чистой, располагается тонкий лепесток полимерной пленки. Хорошо, если его толщина будет не более 5 микрон. На поверхность лепестка надо посадить каплю воды и наблюдать за происходящим. Кап­ля начнет изгибать пленку, стремясь завернуться в нее. Отчетливо это иллюстрирует кинограмма. Работает при этом та сила, которая на рисунке обозначена жирной стрелкой. Если бы полимерная пленка абсолютно подчи­ нялась воле капли, произошло бы следующее: капля при­няла бы форму сферы, равномерно покрыв себя слоем поли­мерной пленки. В действительности же, так как плоская пленка не может приобрести сферическую форму, капле не удается полностью в нее завернуться, но все же устра­ивается она при этом более удобно, чем на плоской поверх­ности.

Стремление капли завернуться в пленку мы объяснили, сославшись на силу, изображенную жирной стрелкой. Можно и в иных словах и понятиях описать процесс, за­