Поделки из дерева

приобретения опыта по составлению рисунка и орнамента.

Для использования резных колечек в качестве серег нужно проделать в них небольшое отверстие и вдеть в них крючочки от недорогих покупных серег. Кстати, неплохо заодно продумать и такой вариант: купить серьги, для которых выполненные колечки будут оригинальным обрамлением. Конечно, это вопрос инициативы и выдумки мастера (рис. 17).

Оригинальные декоративные цепочки делают и вручную, не используя для выполнения колец электрическую дрель или токарный станок. Причем вручную удается вырезать уже собранные цепочки, то есть цепочки, звенья которых получаются соединенными в процессе их изготовления (см. рис. 12, а). Конечно, у таких цепочек лучше делать крупные звенья, чтобы было удобнее с ними работать. Как видно из рисунка, сначала придется подготовить для цепочки заготовку с крестообразным сечением. Четверти в такой заготовке выбираются либо специальным рубанком (зензубелем, фальцгебелем), либо вручную с помощью полукруглой и прямой стамесок.

Затем на заготовке вычерчиваются звенья цепочки, которые в дальнейшем высверливаются по внутреннему контуру дрелью и окончательно дорабатываются ножом. Заметим, что звено отделяется от заготовки только тогда, когда уже обработана вся остальная часть звена. Это понятно, так как пока звено соединено с заготовкой, его удобнее и точить и шлифовать.

Рис. 17. Серьги, выполненные из древесины вручную, а также с токарной обработкой на приставке к дрели

Для таких цепочек с крупными звеньями больше всего подходит древесина с четкой текстурой, например лиственницы, сосны, ели, вишни.

Необычно смотрится цепочка из витых звеньев, похожих по форме на пропеллер. В сборе цепочка выглядит плоской. Каждое звено ее вытачивается на конце круглой палочки- заготовки и отрезается от заготовки только тогда, когда оно по возможности полностью обработано и отшлифовано (см. рис. 12, в).

Монтируется цепочка из витых звеньев так же, как и цепочка из круглых звеньев, то есть путем разлома одного из звеньев. Конечно, если цепочка делается из сырой, пружинящей древесины, лучше ограничиться расколом звена только в одном месте, так как очень трудно стянуть как-либо две половинки витого звена при склеивании и обычно приходится прижимать их друг к другу руками.

В качестве материала для такой цепочки можно взять буковую палочку или криволинейный сучок можжевельника. С витой цепочкой хорошо работать во время отдыха на природе, так как все можно делать ножами и шкуркой.

Фигурные звенья (см. рис. 12, г) обычно выпиливают лобзиком из плоских заготовок: дощечек, реек, многослойной фанеры. Кроме соединения цепочки с помощью разлома, можно крупные звенья и распиливать, причём для фанеры последний способ обязателен. Нет необходимости во всех случаях распиливать соединяющие звенья на две части. Можно, например, выпилить с одной стороны звена кусочек для прохода других звеньев, а затем вклеить его. Тонкие пропилы лобзиком не создадут заметной помехи при стягивании кольца резинкой или шнуром.

Звездчатый кристалл «ежик» и звездчатый шар. Изображенный на рис. 18, а многогранник – малый звездчатый додекаэдр. Необыкновенно красивая симметричная форма многогранника делает его своеобразным декоративным украшением. Оригинальность многогранника- кристалла заключается в том, что его пятиконечные звезды имеют общие концы с такими же соседними звездами. То есть, глядя на конец звезды, мы мысленно можем его связать с одной или со второй звездой, и так равномерно по всей поверхности кристалла.

Рис 18. Звездчатый кристалл (додекаэдр) и звездчатый шар, выполненные из заготовок одного размера. Звездчатый кристалл – женское украшение

Рис. 19. Построение вершин звездчатого додекаэдра на поверхности шара

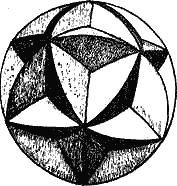
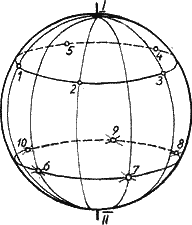
На первых порах пугает сложность изготовления такого многогранника, а вернее, сложность предстоящей разметки вершин и граней пятиконечных звезд. Однако разметка не так уж сложна, если в качестве исходной заготовки при выполнении кристалла в дереве использовать правильный шар. Тогда разбивку 12 вершин пятиконечных звезд можно представить следующим образом (рис. 19): 2 вершины полюса на противоположных сторонах шара и по 5 вершин на двух поясах – параллелях шара Именно уровень этих двух поясов, а значит, и их диаметр определяют успех дела: если разделить каждую параллель на 5 частей с целью получить положение 5 вершин звезд, то расстояния между ними должны быть такими же, как и расстояния каждой из них до первой вершины звезды, расположенной на полюсе. Заметим, что вершины звезд на параллели в нижней части шара должны быть расположены не на одних меридианах с вершинами звезд на верхнем поясе, а строго между ними.

Сначала замерим длину экватора на шаровой заготовке, обогнув ее полоской бумаги. Если разделить полученную длину на коэффициент 5,86, то получится искомое расстояние между вершинами звезд на шаре. Теперь, взяв это расстояние циркулем, проведем в любом месте на его поверхности окружность, которая будет первым поясом – параллелью, и этим же размером циркуля разделим полученную окружность на 5 частей (центр окружности станет «северным полюсом»).

Определив вершины звезд в «северном полушарии», можно таким же способом найти положение вершин и в «южном полушарии». Однако мы не знаем места южного полюса. Конечно, его тоже можно построить, но проще из каждой точки деления на первом поясе сделать тем же размером циркуля эасечка в сторону второго пояса, то есть получить тем самым положение вершин звезд на втором поясе. А откладывая из полученных точек все те же расстояния, можно найти и другой полюс шара. Вероятно, из-за неточности коэффициента и самой шаровой поверхности мы получим при этом не одну, а несколько точек, в центре которых и будет искомый полюс. Теперь, ведя построение в обратном направлении, легко внести исправления допущенных погрешностей.

Дальнейшее выполнение звездчатого кристалла будет несложным: нужно вырезать трехгранные углубления между каждыми тремя смежными вершинами. Эти углубления формируют объемные концы пятиконечных звезд.

Но здесь могут быть два технических решения. Одно из них – сделать стенки трехгранного углубления плоскими, а ребра прямыми. Значит, следуя этому решению, лучше сначала сделать между вершинами звезд плоские срезы шара. В этих плоскостях и будут лежать прямые линии – верхние ребра концов звезд. Таким образом мы превращаем шар в многогранник.

При выполнении трехгранных углублений будем ориентироваться на то, что вершина каждого такого углубления (пирамиды) находится посередине между вершинами звезд, то есть все грани одинаковы. А глубина выемки делается такой, что после выполнения всех пяти выемок вокруг вершины звезды должна образоваться общая единая плоскость, на которой лежит звезда.

Можно также сохранить ливню каждого конца звезды как дугу, лежащую на поверхности шара. Для