Другая история науки. От Аристотеля до Ньютона

О математике Древнего Египта

Все наши познания о древнеегипетской математике основаны главным образом на двух больших папирусах математического характера и на нескольких небольших отрывках.

Один из больших папирусов носит название математического папируса Ринда (по имени обнаружившего его ученого) и находится в Лондоне. Он имеет приблизительно 5,5 метра в длину и 32 сантиметра в ширину. Другой большой папирус, почти такой же длины и 8 сантиметров в ширину, находится в Москве. Содержащиеся в них математические сведения относят примерно к 2000 году до н. э.

Папирус Ринда содержит 84 задачи прикладного характера. При решении этих задач производятся действия с дробями, вычисляются площади прямоугольника, треугольника, трапеции и круга, объемы параллелепипеда, цилиндра, размеры пирамид. Имеются также задачи на пропорциональное деление, а при решении одной задачи находится сумма геометрической прогрессии.

В Московском папирусе собраны решения 25 задач. Большинство их такого же типа, как и в папирусе Ринда. Кроме того, в одной из задач правильно вычисляется объем усеченной пирамиды с квадратным основанием, а в другой содержится самый ранний в математике пример определения площади кривой поверхности: вычисляется боковая поверхность корзины, то есть полуцилиндра, высота которого равна диаметру основания.

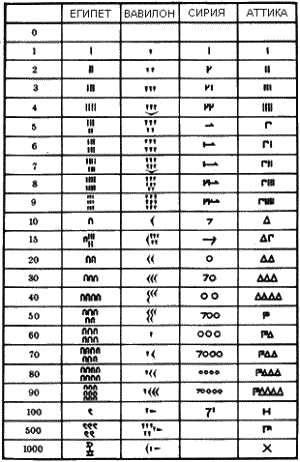
При изучении этих папирусов обнаруживается, что у древних египтян сложилась определенная система счисления: десятичная иероглифическая. Для узловых чисел вида 10к (к = 0, 1, 2,…, 7) установлены индивидуальные иероглифы. Алгоритмические числа записывались комбинациями узловых чисел. С помощью этой системы египтяне справлялись со всеми вычислениями, в которых употребляются целые числа. Что касается дробей, то египтяне понимали дроби только как доли единицы: употреблялись лишь дроби аликвотные (вида 1/n) и некоторые индивидуальные, как, например, 2/3, 3/4. Все результаты, которые должны были выражаться дробями вида т/n, выражались суммой дробей. Для облегчения этих операций были составлены специальные таблицы, например таблица чисел вида 2/n (n = 3,…, 101).

Сложились также определенные приемы производства математических операций с целыми числами и дробями. При умножении, например, преимущественно используется способ постепенного удвоения одного из сомножителей и складывания подходящих частных произведений (отмечены звездочкой) (12 ? 12)

1 – 12

2 – 24

*4 – 48

*8 – 96

Вместе – 144

При делении также используется процедура удвоения и последовательного деления пополам. Деление, по-видимому, было самой трудной математической операцией для египтян; в нем наблюдается самое большое разнообразие приемов.

Цифры Египта, Вавилона, Сирии и Аттики

Приведем пример одной из задач.

«Сало. Годовой сбор 10 беша. Какой ежедневный сбор? Обрати 10 беша в ро. Это будет 3200. Обрати год в дни. Это будет 365. Раздели 3200 на 365. Это 8 2/3 1/10 1/2190. Обрати».

Производится постепенный подбор частного. 8 дает разницу между истинным и частичным делимым: 3200–2920 = 280. Сомножитель 2/3 дает: 365 ? 2/3 = 243 1/3. Еще до 280 не хватает 36 2/3. Очередной подбор 1/10 дает уже разницу в 1/6 (так как 36 2/3-36 1/2 = 1/6). Остается только подобрать число, которое, будучи умножено на 365, дало бы 1/6. Это 1/2190. Таким образом, частное отыскивается постепенным подбором, для которого еще нет единого метода.

Часто встречается операция, называемая «хау» («куча»), соответствующая решению линейного уравнения вида ах + bх +… сх = d.

Материалы, содержащиеся в папирусах, позволяют утверждать, что в Египте начали складываться элементы математики как науки. Техника вычислений еще примитивна, методы решения задач неединообразны.

Византийская математика

Основным достижением математической мысли, характеризующим начало византийской математики, было возникновение и развитие понятия о доказательстве. Первым из философов, применившим в математике метод доказательства, считается греческий ученый Фалес из Милета. Фалес доказал, например, равенство вертикальных углов, равенство углов при основании равнобедренного треугольника, один из признаков равенства треугольников и т. д.

Новым было то, что Фалес впервые попытался логически свои выводы обосновать. Тем самым он положил начало дедуктивной математики – той, которая впоследствии была превращена в стройную и строгую систему знаний.

Затем метод доказательства был усовершенствован и развит учеными пифагорейской школы, которые доказали, в частности, утверждение, называемое теперь теоремой Пифагора. Пифагорейцы предприняли первую попытку свести геометрию и алгебру того времени к арифметике. Они считали, что «все есть число», понимая под словом «число» лишь натуральные числа.

Однако натуральных чисел и дробей оказалось недостаточно для того, чтобы выразить длину диагонали квадрата со стороной 1. Анализ полученного доказательства привел к исследованию начальных вопросов теории чисел (четности и нечетности натуральных чисел, разложения чисел на простые множители, свойств взаимно простых чисел и т. д.). Византийские математики эллинского периода предприняли попытку обосновать всю математику на основе геометрических понятий. Они истолковывали, например, сложение величин как сложение отрезков, а умножение – как построение прямоугольника с заданными сторонами.

Недостатком геометрического подхода к математике было то, что он препятствовал развитию алгебры. Византийцы умели в геометрической форме решать квадратные уравнения, но невозможно было представить геометрически четвертую и высшие степени длины, а кроме того, нельзя было складывать выражения разных степеней: эта сумма геометрического смысла не имела. По той же причине в византийской математике не было отрицательных чисел и нуля, иррациональных чисел и буквенного исчисления.

Пифагор первый заметил, что сила и единство науки основаны на работе с идеальными объектами. Например, прямая линия – это не тетива натянутого лука и не луч света: ведь они имеют небольшую толщину, а линия толщины не имеет. То же относится к геометрической плоскости и поверхности воды в спокойном озере или к числу 5 и пяти пальцам на руке. Идеальные объекты (будь то числа или фигуры) встречаются только в математическом рассуждении.

Все природные тела и процессы суть искаженные подобия идеальных тел и движений, а закономерности идеальных объектов выражаются с помощью чисел. Короче говоря: числа правят миром через свойства геометрических фигур! Но если так, то любые свойства чисел приобретают особое (даже мистическое) значение. Есть числа четные, а есть нечетные; есть простые и есть составные. И еще есть дроби, то есть отношения натуральных чисел; их Пифагор из осторожности называл не числами, а «величинами».

Так в школе Пифагора из арифметики была выделена в отдельную область теория чисел, то есть совокупность математических знаний, относящихся к общим свойствам операций с натуральными числами. В это время уже стали известными способы суммирования простейших арифметических прогрессий. Были рассмотрены вопросы делимости чисел, введены арифметическая, геометрическая и гармоническая пропорции.

Наряду с геометрическим доказательством теоремы Пифагора был найден способ отыскания неограниченного ряда троек «пифагоровых» чисел, то есть троек чисел, удовлетворяющих соотношению a ² + b ² = c ² и имеющих вид: п, (n ²-1)/2, (n ² + 1)/2, где п – нечетное. Было открыто много математических закономерностей теории музыки.