Сборник задач по математике с решениями для поступающих в вузы

найдите точку P, сумма расстояний которой от вершин А, В и С была бы наименьшей.

2.10. Постройте прямоугольный треугольник по данной гипотенузе с и биссектрисе l прямого угла.

2.11. Постройте четырехугольник, если известны три его стороны и два внутренних острых угла, прилежащих к четвертой стороне.

2.12. Из данной точки M, лежащей вне круга, проведите секущую так, чтобы внешняя ее часть равнялась внутренней.

2.13. Через точку пересечения двух окружностей проведите секущую так, чтобы отрезок ее, заключенный внутри окружностей, имел данную длину а.

2.14. Через точку M внутри окружности проведите хорду так, чтобы разность ее отрезков равнялась данному отрезку.

2.15. Даны окружность, ее хорда CD и две точки А и В окружности, лежащие по одну сторону от CD. На этой окружности постройте точку M так, чтобы хорды AM и BM высекали на CD отрезок PQ заданной длины а.

2.16. Даны окружность, две ее точки А и В, секущая и точка M, лежащая на ней внутри окружности. Найдите на окружности такую точку С, чтобы прямые AC и BC высекали на данной секущей отрезок, делящийся в точке M пополам.

2.17. Постройте окружность, проходящую через данные точки А и В и касающуюся данной прямой PQ.

2.18. Пользуясь только линейкой, опустите перпендикуляр из точки M, лежащей вне окружности, на данный диаметр окружности (или на его продолжение).

2.19. Пользуясь только линейкой, опустите перпендикуляр из точки M, лежащей на окружности, на данный диаметр окружности.

2.20. Точки А и В лежат по разные стороны прямой l. Найдите на ней такую точку С, чтобы величина |AC ? BC| была наибольшей.

2.21. Дан выпуклый четырехугольник, не являющийся квадратом. Постройте описанный около него квадрат так, чтобы на каждой стороне квадрата лежала одна вершина четырехугольника.

2.22. Дан отрезок длины 7. С помощью циркуля и линейки постройте отрезок длины v7.

2.23. Даны два отрезка: длины 1 и длины 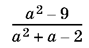а. С помощью циркуля и линейки постройте отрезок длины .

Глава 3 Геометрические задачи в пространстве

Прежде чем приступить к решению стереометрических задач, обратите внимание на следующие определения и теоремы.

Признак перпендикулярности прямой и плоскости и теорему о трех перпендикулярах нужно формулировать так:

Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости.

Если проекция наклонной на плоскость перпендикулярна к прямой, лежащей в этой плоскости, то и сама наклонная перпендикулярна к этой прямой.

Требование, чтобы прямые, лежащие в плоскости, и прямая, перпендикулярная к этим прямым, проходили через общую точку, излишне. Точно так же не следует требовать, чтобы наклонная, о которой идет речь в теореме о трех перпендикулярах, и прямая, лежащая в плоскости, проходили через общую точку.

Расстоянием между двумя прямыми AB и CD называется наименьшее из расстояний между двумя точками, одна из которых принадлежит AB, а другая — CD.

Две прямые называются параллельными, если через них можно провести плоскость и они не пересекаются.

Две прямые называются скрещивающимися, если через них нельзя провести плоскость.

Расстоянием между двумя скрещивающимися прямыми является длина отрезка, высекаемого ими на прямой, перпендикулярной к обеим скрещивающимся прямым.

Последнее утверждение является теоремой, а не определением, и может быть доказано.

Во всех последующих задачах рассматриваются только выпуклые многогранники, т. е. такие, которые лежат по одну сторону от любой из его граней. Грани рассматриваемых многогранников являются выпуклыми многоугольниками.

Призмой называется многогранник, в котором две грани — равные многоугольники с соответственно параллельными сторонами, а остальные грани пересекаются между собой по прямым, параллельным друг другу.

Второе требование в этом определении нельзя заменить условием: «остальные грани — параллелограммы», так как иначе пришлось бы отнести к призмам многогранник, составленный из двух равных наклонных параллелепипедов, симметричных относительно плоскости их общего основания, крест, образованный из пяти равных кубиков и m. n.

Если боковые ребра (грани) пирамиды одинаково наклонены к плоскости основания, то высота пирамиды проецируется в центр описанной вокруг основания (вписанной в основание) окружности.

Если боковые ребра и грани пирамиды одинаково наклонены к плоскости основания, то пирамида правильная.

Площадь ортогональной проекции многоугольника на плоскость P равна произведению площади этого многоугольника на косинус угла между плоскостью многоугольника и плоскостью P.

Если все боковые грани пирамиды наклонены к основанию под углом  ?, то S_{основания} = S_{боковой поверхности} ·cos ?.

Треугольную пирамиду называют тетраэдром.

Правильным тетраэдром называется тетраэдр, у которого все ребра равны.

В задачах рассматриваются только прямые круговые конусы и цилиндры.

Конус (цилиндр) называется равносторонним, если его осевое сечение есть правильный треугольник (квадрат).

3.1. Через точку, лежащую на ребре двугранного угла ? (0 < ? < ^?/₂), проходят два луча, расположенных в различных полуплоскостях его. Один из этих лучей перпендикулярен к ребру, а другой образует с ребром острый угол ?. Найдите угол между данными лучами.