выборки.
Статистиками разработано много различных мер взаимосвязи между переменными. Выбор определенной меры в конкретном исследовании зависит от числа переменных, используемых шкал измерения, природы зависимости и т.д. Большинство таких мер между переменными подчиняется общему принципу статистической значимости: оценивание наблюдаемой зависимости с помощью сравнения ее с максимально мыслимой зависимостью – критерием. Значение статистических критериев состоит в оценивании зависимости между переменными. Однако, чтобы определить уровень статистической значимости, нужна функция, которая представляла бы зависимость между «величиной» и «значимостью» зависимости между переменными для каждого объема выборки. Большинство функций имеет характер нормального распределения (рис. 40), представляющего собой одну из эмпирически проверенных истин общей природы статистически значимого числа объектов и один из фундаментальных законов природы. Форма нормального распределения – характерная колоколообразная кривая – определяется двумя параметрами: средним и стандартным отклонением. Более точную информацию о форме распределения можно получить с помощью критериев нормальности. Однако ни один из критериев не может заменить визуальную проверку нормальности с помощью гистограммы (частоты попаданий значений переменной в отдельные интервалы).
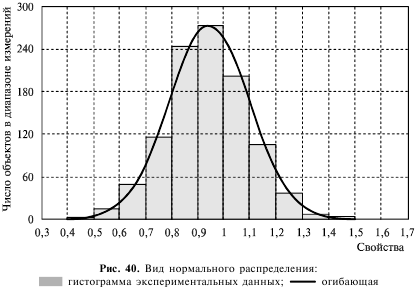
Гистограмма позволяет качественно и наглядно оценить различные характеристики распределения, на нее может накладываться кривая нормального распределения. Например, если асимметрия существенно отличается от 0, то распределение несимметрично, в то время как нормальное распределение абсолютно симметрично, а его асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна. На гистограмме можно увидеть, к примеру, что распределение бимодально (имеет 2 пика), это может быть вызвано тем, что выборка неоднородна, возможно, извлечена из двух разных по свойствам, каждая из которых более или менее нормальна. В таких ситуациях, чтобы понять природу наблюдаемых переменных, можно попытаться найти качественный способ разделения выборки на две части.
При возрастании объема выборки форма выборочного распределения приближается к нормальной, даже если распределение исследуемых переменных не является нормальным. Центральная предельная теорема гласит, что при размере выборки
Важным способом описания переменной является форма ее распределения, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Эти интервалы, называемые интервалами группировки, выбираются исследователем, которого интересует, насколько точно распределение можно аппроксимировать нормальным. Характерное свойство нормального распределения состоит в том, что 68% всех его наблюдений лежат в диапазоне ±1 стандартного отклонения от среднего, а диапазон ±2 стандартных отклонения содержит 95% значений. Другими словами, при нормальном распределении стандартизованные наблюдения меньше–2 или больше +2 имеют относительную частоту менее 5%.
Для характеристики меры изменчивости распределения используют показатель вариации или стандартное отклонение, представляющее собой корень квадратный из дисперсии:
Иногда используют стандартизованное наблюдение, которое означает, что из исходного значения вычтено среднее и результат поделен на стандартное отклонение.
Исследователю часто бывают необходимы такие статистики, которые позволяют сделать вывод относительно свойств генеральной выборки в целом. Для этого используются описательные статистики, оперирующие такими понятиями, как истинное среднее и доверительный интервал. Среднее генеральной выборки является информативной мерой положения наблюдаемой переменной в доверительном интервале. Доверительный интервал представляет собой интервал, в котором с заранее выбранной вероятностью, близкой к единице (меньшей единицы на величину выбранного уровня значимости критерия), можно утверждать, что с данным уровнем доверия находится истинное значение оцениваемого параметра. Ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной.
Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем

95% интервал с границами 19 и 27 накрывает среднее генеральной выборки. Если установить больший уровень доверия, то интервал станет шире, возрастет вероятность, с которой он накрывает неизвестное среднее генеральной выборки, и наоборот. Известно, что чем неопределеннее прогноз погоды (т.е. шире доверительный интервал), тем вероятнее, что он будет правильным. Увеличение разброса наблюдаемых значений уменьшает надежность оценки. Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок. При увеличении объема выборки, скажем, до 100 или более качество оценки улучшается и без предположения о нормальности выборки [237].
Во многих областях исследований точное измерение переменных само по себе представляет сложную задачу, например в психологии точное измерение личностных характеристик или отношений к чему–либо. В целом, очевидно, во всех социальных дисциплинах ненадежные измерения будут препятствовать попытке правильно предсказать результат. В прикладных исследованиях, когда наблюдения над переменными затруднены, важна точность измерений.
Надежность и точность позволяют построить шкалы измерений или улучшить используемые с помощью классической теории тестирования. В этом контексте надежность понимается непосредственно: измерение является надежным, если его основную часть по отношению к погрешности составляет истинное значение. Оценивание надежности шкалы основано на корреляциях между индивидуальными позициями или измерениями, составляющими шкалу, и дисперсиями этих позиций. Показатель разброса некоторого множества результатов измерений вокруг среднего арифметического называется дисперсией, величина которой определяется по формуле:

где X – число правильно выполненных заданий
Каждое измерение (ответ на вопрос) включает в себя как истинное значение, так и частично не контролируемую, случайную погрешность. Для эффективного функционирования контрольно–оценочной системы необходимы высокая надежность и валид–ность педагогических измерений. Под надежностью понимают точность измерений, а также устойчивость результатов к действию случайных факторов. Тест считается надежным, если он обеспечивает высокую точность измерений, а также дает при повторном выполнении на той же выборке близкие результаты при условии того, что подготовка испытуемых не изменилась за время до повторного выполнения теста.
На протяжении десятилетий вопросы надежности исследовались многочисленными теоретиками и практиками в области педагогических измерений. Особо следует отметить работу R.L. Linn [241], в которой рассматриваются не только процедуры оценки надежности, но и методологические вопросы обоснования качества тестовых измерений. Его подход оправдан тем, что в требовании проверки теста на надежность реализуется важная идея методологического характера, связанная с неизбежностью ошибок измерения, порождаемых группой случайных факторов. В самой общей трактовке надежность тестов можно рассматривать как характеристику существующих различий между результатами педагогических измерений и истинными баллами испытуемых (подготовленностью) в той мере, в какой эти различия порождаются случайными ошибками измерения. В теории педагогических измерений ошибка трактуется как статистическая величина, отражающая степень отклонения наблюдаемого балла от истинного балла ученика или студента.
Существование ошибки измерения закладывается и привносится в теорию педагогических измерений основными аксиомами классической теории тестов. К числу наиболее важных аксиом, закладывающих научный фундамент обоснования теории надежности тестов, можно отнести равенство:

