Апории Зенона и проблема движения

А. М. Анисов Апории Зенона и проблема движения

Нашей целью будет не реконструкция зеноновских аргументов, а стремление понять с точки зрения современной науки, на какие реальные трудности в анализе движения указал Зенон Элейский. Именно указал, поскольку о попытке приписать непосредственно Зенону современную постановку проблем движения не может быть и речи. Кстати говоря, эта постановка в логико-философской литературе не отличается единством. Нередко ответственность за парадоксы движения возлагается на неточность и размытость используемых понятий [1]. Уточним понятия – парадоксы исчезнут. Мы с этим не согласны. Апории Зенона касаются самих основ человеческого миропонимания. Они требуют не просто уточнения понятий, а выбора философской платформы объяснения реальности. Поскольку дело построения таких платформ не может быть завершено, пока существует мыслящий разум, на выборе одной из них лежит печать неизбежной исторической ограниченности. Сказанное, разумеется, в полной мере относится и к построениям в данной статье. Но сегодня, несомненно, мы понимаем и знаем больше, чем два с половиной тысячелетия назад, а завтра, возможно, удастся продвинуться вперед еще дальше [2].

Начнем рассмотрение зеноновских затруднений с апорий о движении.

Ахилл и черепаха

Ахилл – герой и, как бы мы сейчас сказали, выдающийся спортсмен. Черепаха, как известно, одно из самых медлительных животных. Тем не менее Зенон утверждал, что Ахилл проиграет черепахе состязание в беге. Примем следующие условия. Пусть Ахилла отделяет от финиша расстояние 1, а черепаху – ?. Двигаться Ахилл и черепаха начинают одновременно. Пусть для определенности Ахилл бежит в 2 раза быстрее черепахи. Тогда, пробежав расстояние ?, Ахилл обнаружит, что черепаха успела за то же время преодолеть отрезок ? и по-прежнему находится впереди героя. Далее картина повторяется: пробежав четвертую часть пути, Ахилл увидит черепаху на одной восьмой части пути впереди себя и т. д. Следовательно, всякий раз, когда Ахилл преодолевает отделяющее его от черепахи расстояние, последняя успевает уползти от него и по-прежнему остается впереди. Таким образом, Ахилл никогда не догонит черепаху. Начав движение, Ахилл никогда не сможет его завершить.

Знающие математический анализ обычно указывают, что ряд

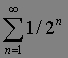
сходится к 1. Поэтому, дескать, Ахилл преодолеет весь путь за конечный промежуток времени и, безусловно, обгонит черепаху [3]. Но вот что пишут по данному поводу Д. Гильберт и П. Бернайс:

“Обычно этот парадокс пытаются обойти рассуждением о том, что сумма бесконечного числа этих временных интервалов все-таки сходится и, таким образом, дает конечный промежуток времени. Однако это рассуждение абсолютно не затрагивает один существенно парадоксальный момент, а именно парадокс, заключающийся в том, что некая бесконечная последовательность следующих друг за другом событий, последовательность, завершаемость которой мы не можем себе даже представить (не только физически, но хотя бы в принципе), на самом деле все-таки должна завершиться” [4] .

Принципиальная незавершаемость данной последовательности заключается в том, что в ней отсутствует последний элемент. Всякий раз, указав очередной член последовательности, мы можем указать и следующий за ним. Интересное замечание, также указывающее на парадоксальность ситуации, встречаем у Г. Вейля:

“Представим себе вычислительную машину, которая выполняла бы первую операцию за ? минуты, вторую – за ? минуты, третью – за ? минуты и т. д. Такая машина могла бы к концу первой минуты “пересчитать” весь натуральный ряд (написать, например, счетное число единиц). Ясно, что работа над конструкцией такой машины обречена на неудачу. Так почему же тело, вышедшее из точки А, достигает конца отрезка В, “отсчитав” счетное множество точек А₁, А₂,…, А_n,…?” [5]

Древние греки тем более не могли себе представить завершенную бесконечную совокупность. Поэтому вывод Зенона о том, что движение из-за необходимости “пересчитать” бесконечное число точек не может закончиться, еще тогда произвел большое впечатление. На схожих аргументах основывается апория о невозможности начать движение.

Дихотомия

Рассуждения очень простое. Для того, чтобы пройти весь путь, движущееся тело сначала должно пройти половину пути, но чтобы преодолеть эту половину, надо пройти половину половины и т. д. до бесконечности. Иными словами, при тех же условиях, что и в предыдущем случае, мы будем иметь дело с перевернутым рядом точек: (?)ⁿ,…, (?)³, (?)², (?) ¹. Если в случае апории Ахилл и черепаха соответствующий ряд не имел последней точки, то в Дихотомии этот ряд не имеет первой точки. Следовательно, заключает Зенон, движение не может начаться. А поскольку движение не только не может закончиться, но и не может начаться, движения нет. Существует легенда, о которой вспоминает А. С. Пушкин в стихотворении «Движение»:

Движенья нет, сказал мудрец брадатый.

Другой смолчал и стал пред ним ходить.

Сильнее бы не мог он возразить;

Хвалили все ответ замысловатый.

Но, господа, забавный случай сей

Другой пример на память мне приводит:

Ведь каждый день пред нами солнце ходит,

Однако ж прав упрямый Галилей.

Действительно, согласно легенде, один из философов так и “возразил” Зенону. Зенон велел бить его палками: ведь он не собирался отрицать чувственное восприятие движения. Он говорил о его немыслимости, о том, что строгое размышление о движении приводит к неразрешимым противоречиям. Поэтому, если мы хотим избавиться от апорий в надежде, что это вообще возможно (а Зенон как раз считал, что невозможно), то мы должны прибегать к теоретическим аргументам, а не ссылаться на чувственную очевидность. Рассмотрим одно любопытное теоретическое возражение, которое было выдвинуто против апории Ахилл и черепаха.

“Представим себе, что по дороге в одном направлении движутся быстроногий Ахилл и две черепахи, из которых Черепаха-1 несколько ближе к Ахиллу, чем Черепаха-2. Чтобы показать, что Ахилл не сможет перегнать Черепаху-1, рассуждаем следующим образом. За то время, как Ахилл пробежит разделяющее их вначале расстояние, Черепаха-1 успеет уползти несколько вперед, пока Ахилл будет пробегать этот новый отрезок, она опять-таки продвинется дальше, и такое положение будет бесконечно повторяться. Ахилл