Сборник задач по математике с решениями для поступающих в вузы

⁸¹/_{4x? + 36x + 81} > 1 + 2x.

Умножим неравенство на знаменатель, который при x > 0 положителен; после приведения подобных получим систему

Итак, в первом случае неравенство имеет решения: 0 < x < ⁴⁵/₈.

При x = 0 данное неравенство не удовлетворяется.

Если же x < 0, то, умножив обе части на ?1, придем к неравенству

Проделав с этим неравенством преобразования, аналогичные случаю, когда x > 0, придем к выводу, что оно не имеет решений при отрицательных x.

Ответ. 0 < x < ⁴⁵/₈.

10.25. Перепишем данное неравенство в виде

т. е.

Обозначив выражение, стоящее в скобках, через y, получим квадратное неравенство

y? + y ? 42 < 0,

которое имеет решения: ?7 < y < 6. Итак,

Поскольку сумма  всегда положительна, то достаточно решить лишь правое неравенство:

После возведения в квадрат получим неравенство

равносильное исходному, так как корни vx и  здесь не устранены. (Заметьте, что, заменив выражение vx  на  мы могли нарушить равносильность.) После второго возведения в квадрат придем к системе

Ответ. 0 ? x < ⁸⁴¹/₁₄₄.

10.26. Неравенство удобно переписать в виде

Оно равносильно совокупности двух систем

Решая последнее неравенство каждой из систем, найдем ?|а| ? x ? |а|.

Так как в первой системе x > 0, то для нее получим решения:

0 < x ? |а|, а ? 0.

Перейдем ко второй системе. Решая второе неравенство, получим

?^|а|/_v5 < x < ^|а|/_v5.

Мы приходим к системе

решениями которой будут значения из интервала ?^|а| /_v5 < x ? 0  при а ? 0. Остается объединить решения двух систем.

Ответ. При а ? 0: ?^|а| /_v5 < x ? |а|; при а = 0 неравенство не имеет решений.

10.27. Приведем степени, входящие в данное неравенство, к основанию 2 и поделим на 2^vx 2^x:

2^{x ? vx} ? 3 + 4 · 2^{vx ? x};

обозначив 2^{x ? vx} = y, получим

y ? 3 + ⁴/_y,

а так как y > 0, то

y? ? 3y ? 4 ? 0.

Корни трехчлена: ?1, 4; так как меньший корень отрицателен, то получаем

2^{x ? vx} ? 4,

т. е. x ? vx ? 2. Обозначим vx = z и найдем решения неравенства

z? ? z ? 2 ? 0.

Получим ?1 ? z ? 2. Левое неравенство выполняется, если только vx существует. Остается vx ? 2, т. е. 0 ? x ? 4.

Ответ. 0 ? x ? 4.

10.28. Перепишем неравенство в виде

3^vx(3 + x ? 2x?) ? 2(?2x? + x + 3) < 0,

или

(3^vx ? 2)(?2x? + x + 3) < 0.

Последнее неравенство[20] равносильно совокупности систем

Решая первую систему, получим

Так как ?1 < 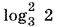 < = 1 < ³/₂, то окончательно получим x > ³/₂.

Вторая система дает нам следующее:

Ответ.

10.29. Если x > 0, то неравенство равносильно такому:

^{(x ? 1)2x ? 1}/_{3 ? x} < 0, т. е. ^{(x ? 1)(x ? ?)}/_{x ? 3} > 0.

Воспользовавшись методом интервалов, получим ? < x < 1, x > 3. Если x = 0, то левая часть неравенства обращается в выражение 0^?? , которое не имеет смысла.

При x < 0 показатель степени должен быть целым числом, т. е.